Question

证明“在△ABC中，如果AB=c，BC=a，AC=b，且∠C=90°，那么a²+b²=c²”是真命题．

Answer 1

考点：命题与定理,勾股定理

专题：

分析：以a，b长为上下底边，以a+b长为高，作梯形ABDE，即AB⊥BD，ED⊥BD，AB=a，ED=b，在其高BD上再取一点C，使BC=b，连结AC，EC，求出△ACE是等腰直角三角形，根据梯形面积公式求出梯形面积，根据三角形面积公式求出梯形面积，即可得出等式，即可得出答案．

解答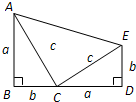：证明：在△ADE和△EBC中，

AD=EC ∠C=∠D=90° DE=BC

，
∴△ADE≌△EBC（SAS），
∴∠AED=∠CBE，
∵∠CBE+∠BEC=90°，
∴∠AED+∠BEC=90°，
∴∠AEB=90°，
∴梯形的面积=

1

2

（a+b）（a+b）=2×

1

2

ab+

1

2

c²，
整理得a²+b²=c²．
∴在△ABC中，如果AB=c，BC=a，AC=b，且∠C=90°，那么a²+b²=c²是真命题．

点评：本题考查了勾股定理的证明，全等三角形的判定与性质，求出∠AEB=90°是解题的关键，难点在于利用梯形的面积列出方程．