题目内容
11.若直线l1:y=k1x+b1与l2:y=k2x+b2的交点在直线l上,则把直线l叫做l1、l2的“轨线”.(1)求l1:y=-x+3m-1与l2:y=x+m-1的“轨线”l的解析式;
(2)若l1:y=2x+b1与l2:y=-2x+b2的交点在y=x+2上,且l1、l2的“轨线”为y=-x,求l1、l2的解析式.
(3)若l1:y=k1x+b1与l2:y=k2x+b2分别满足k1+b1=0,3k2+b2=2.
①求证:l1、l2分别经过两个定点A、B;
②若l1、l2的交点为C,且S△ABC=2,求l1、l2的“轨线”的解析式.
分析 (1)由$\left\{\begin{array}{l}{y=-x+3m-1}\\{y=x+m-1}\end{array}\right.$,消去m可得y=2x-1,根据“轨线”的定义可知,l1:y=-x+3m-1与l2:y=x+m-1的“轨线”l的解析式为y=2x-1;
(2)由$\left\{\begin{array}{l}{y=x+2}\\{y=-x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,由题意点(-1,1)在l1:y=2x+b1与l2:y=-2x+b2上,可得b1=3,b2=-1;
(3)①只要证明A(1,0),B(3,2)分别在直线l1、l2上即可;
②如图,A(1,0),B(3,2),作BH⊥x轴于H,HM⊥AB于M.易知AB=2$\sqrt{2}$,HM=$\sqrt{2}$,推出S△HAB=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$=2,所以点C在过点H平行AB的直线l上,由直线AB的解析式为y=x-1,所以直线l的解析式为y=x-3,根据对称轴可知,当点C在直线l关于直线AB的对称的直线l′上时,也满足条件;
解答 (1)解:由$\left\{\begin{array}{l}{y=-x+3m-1}\\{y=x+m-1}\end{array}\right.$,消去m可得y=2x-1,
根据“轨线”的定义可知,l1:y=-x+3m-1与l2:y=x+m-1的“轨线”l的解析式为y=2x-1.
(2)解:由$\left\{\begin{array}{l}{y=x+2}\\{y=-x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-1}\\{y=1}\end{array}\right.$,
由题意点(-1,1)在l1:y=2x+b1与l2:y=-2x+b2上,
∴b1=3,b2=-1.
∴l1:y=2x+3与l2:y=-2x-1.
(3)①证明:∵若l1:y=k1x+b1与l2:y=k2x+b2分别满足k1+b1=0,3k2+b2=2.
∴直线l1:y=k1x+b1与l2:y=k2x+b2分经过点A(1,0),B(3,2),
∴l1、l2分别经过两个定点A、B.
②如图,A(1,0),B(3,2),作BH⊥x轴于H,HM⊥AB于M.
易知AB=2$\sqrt{2}$,HM=$\sqrt{2}$,
∴S△HAB=$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{2}$=2,
∴点C在过点H平行AB的直线l上,
∵直线AB的解析式为y=x-1,
∴直线l的解析式为y=x-3,
根据对称轴可知,当点C在直线l关于直线AB的对称的直线l′上时,也满足条件,
易知直线l′的解析式为y=x+1.
∴l1、l2的“轨线”的解析式为y=x-3或y=x+1.
点评 本题考查一次函数的应用、一元一次方程组的应用、两直线平行的判定和性质、三角形的面积等知识,解题的关键是理解题意,学会用转化的思想思考问题,把问题转化为方程组解决,属于中考创新题目.

| A. | 24×10-26kg | B. | 2.4×10-25kg | C. | 0.24×10-24kg | D. | 2.4×10-24kg |
| A. | 垂直 | B. | 平行 | C. | 相交 | D. | 以上都不对 |
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
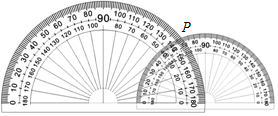 如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为70°.(只考虑小于90°的角度)
如图,小量角器的0°刻度线在大量角器的0°刻度线上,且小量角器的中心在大量角器的外缘边上.如果它们外缘边上的公共点P在大量角器上对应的度数为40°,那么在小量角器上对应的度数为70°.(只考虑小于90°的角度)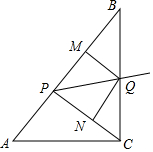 如图,已知在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,ON⊥CP于N.
如图,已知在Rt△ABC中,斜边AB=10,sinA=$\frac{4}{5}$,点P为边AB上一动点(不与A,B重合),PQ平分∠CPB交边BC于点Q,QM⊥AB于M,ON⊥CP于N.