题目内容
1.已知x=2是方程x2+bx-2=0的一个根,则b的值是( )| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
分析 由一元二次方程的解的定义,将x=2代入已知方程列出关于b的新方程,通过解新方程来求b的值即可.
解答 解:根据题意,得
22+2×b-2=0,即2b+2=0,
解得,b=-1.
故选A.
点评 本题考查的是一元二次方程的根即方程的解的定义.一元二次方程的根就是一元二次方程的解,就是能够使方程左右两边相等的未知数的值.即用这个数代替未知数所得式子仍然成立.

练习册系列答案
相关题目
12.在同一平面内,AB⊥l,BC⊥l,B为垂足,那么A、B、C三点在同一条直线上.判断这个命题为真命题的理由是( )
| A. | 两点确定一条直线 | |
| B. | 经过直线外一点,有且只有一条直线与这条直线平行 | |
| C. | 垂线段最短 | |
| D. | 同一平面内,过一点有且只有一条直线与已知直线垂直 |
9.钟表在4点10分时,它的时针和分针所形成的锐角度数是( )
| A. | 65° | B. | 75° | C. | 85° | D. | 90° |
16. 如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )
如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )
 如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )
如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )| A. | 50° | B. | 45° | C. | 40° | D. | 30° |
13.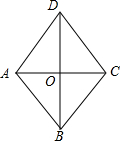 如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )
 如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )
如图,在菱形ABCD中,对角线AC、BD相交于点O,且AC=2,若AB=2,则BD的长为( )| A. | $\sqrt{3}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 2$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
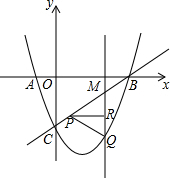 如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m.
如图,抛物线y=ax2-(a+1)x-3与x轴交于点A、B,与y轴交于点C,∠BCO=45°,点M为线段BC上异于B、C的一动点,过点M与y轴平行的直线交抛物线于点Q,点R为线段QM上一动点,RP⊥QM交直线BC于点P.设点M的横坐标为m. 如图所示.在平面直角坐标系xOy中,点A坐标为(6,6).作正方形OBAC,点D坐标为(8,2),作正方形BEDF.连结OA,EF.点P,Q,R分别为OA,EF,OF的中点,连结PQ,PR,QR.
如图所示.在平面直角坐标系xOy中,点A坐标为(6,6).作正方形OBAC,点D坐标为(8,2),作正方形BEDF.连结OA,EF.点P,Q,R分别为OA,EF,OF的中点,连结PQ,PR,QR.