题目内容
7.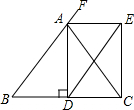 如图所示,△ABC中,AB=AC,AD是BC边上的高,AE是∠CAF的平分线且∠CAF是△ABC的一个外角,且DE∥BA,四边形ADCE是矩形吗?为什么?
如图所示,△ABC中,AB=AC,AD是BC边上的高,AE是∠CAF的平分线且∠CAF是△ABC的一个外角,且DE∥BA,四边形ADCE是矩形吗?为什么?
分析 由角平分线定义得:∠BAD=∠CAD=$\frac{1}{2}$∠BAC和∠CAE=∠FAE=$\frac{1}{2}$∠FAC,则∠DAE=90°,再证明∠AEC=∠ECB=90°,由三个角是直角的四边形是矩形得出结论.
解答 解:是矩形;理由如下:
∵AD是∠BAC的平分线,
∴∠BAD=∠CAD=$\frac{1}{2}$∠BAC,
∵AE是∠BAC的外角的平分线,
∴∠CAE=∠FAE=$\frac{1}{2}$∠FAC,
∵∠BAC+∠FAC=180°,
∴∠DAC+∠EAC=$\frac{1}{2}$×180°=90°,
即∠DAE=90°,
∵CE⊥AE,
∴∠AEC=90°,
∵AB=AC,
∴∠B=∠ACB,
∵∠B+∠ACB+∠BAC=180°,
∴∠B+∠ACB=∠FAE+∠CAE,
∴∠FAE=∠B,
∴AE∥BC,
∴∠AEC+∠ECB=180°,
∴∠ECB=90°,
∴∠DAE=∠AEC=∠ECB=90°,
∴四边形ADCE是矩形.
点评 本题考查了角平分线的定义、等腰三角形的性质及矩形的判定,角平分线可以将一个角分成两个相等的角,同时要熟知等边对等角,掌握矩形的判定:①矩形的定义:有一个角是直角的平行四边形是矩形;②有三个角是直角的四边形是矩形;③对角线相等的平行四边形是矩形;本题利用了第②种判定方法判定四边形ADCE是矩形.

练习册系列答案
相关题目
16.下列说法不正确的是( )
| A. | 3是9的平方根 | B. | 无理数都是无限小数 | ||
| C. | (3-π)2的算术平方根是3-π | D. | 实数与数轴上的点是一一对应的 |
 如图,四边形ABCD是平行四边形,E为边CD延长线上一点,连接BE交边AD于点F.请找出一对相似三角形,并加以证明.
如图,四边形ABCD是平行四边形,E为边CD延长线上一点,连接BE交边AD于点F.请找出一对相似三角形,并加以证明.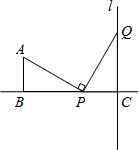 如图,AB=2,BC=5,AB⊥BC于点B,直线l⊥BC于C,点P自点B开始沿射线BC移动,过点P作PQ⊥AP交l于点Q.
如图,AB=2,BC=5,AB⊥BC于点B,直线l⊥BC于C,点P自点B开始沿射线BC移动,过点P作PQ⊥AP交l于点Q.