题目内容
 如图,已知BD,CE分别是△ABC的外角平分线,过点A分别作BD,CE的垂线,交BD,CE于点F,G,交直线BC于点M,N.求证:FG∥MN,FG=
如图,已知BD,CE分别是△ABC的外角平分线,过点A分别作BD,CE的垂线,交BD,CE于点F,G,交直线BC于点M,N.求证:FG∥MN,FG=| 1 |
| 2 |
考点:三角形中位线定理,等腰三角形的判定与性质
专题:证明题
分析:利用“角边角”证明△ABF和△MBF全等,根据全等三角形对应边相等可得AF=MF,AB=MB,同理可得AG=NG,AC=NC,从而得到FG是△AMN的中位线,再根据三角形的中位线平行于第三边并且等于第三边的一半证明即可.
解答:证明:∵BD是△ABC的外角平分线,
∴∠ABF=∠MBF,
∵BD⊥AF,
∴∠AFB=∠MFB=90°,
在△ABF和△MBF中,
,
∴△ABF≌△MBF(ASA),
∴AF=MF,AB=MB,
同理可得AG=NG,AC=NC,
∴FG是△AMN的中位线,
∴FG∥MN,
FG=
(MB+BC+NC),
即FG=
(AB+BC+AC).
∴∠ABF=∠MBF,
∵BD⊥AF,
∴∠AFB=∠MFB=90°,
在△ABF和△MBF中,
|
∴△ABF≌△MBF(ASA),
∴AF=MF,AB=MB,
同理可得AG=NG,AC=NC,
∴FG是△AMN的中位线,
∴FG∥MN,
FG=
| 1 |
| 2 |
即FG=
| 1 |
| 2 |
点评:本题考查了三角形的中位线平行于第三边并且等于第三边的一半,全等三角形的判定与性质,判断出FG是△AMN的中位线是解题的关键,也是本题的难点.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
钟面角是指时钟的时针与分针所成的角.当时间是9:30时,钟面角等于( )
| A、90° | B、102° |
| C、105° | D、120° |
已知a≠0,下列计算正确的是( )
| A、a2+a3=a5 |
| B、a2•a3=a6 |
| C、a3÷a2=a |
| D、(a2)3=a5 |
 如图,△ABC中,∠C=60°,剪去这个60°角后,得到一个四边形,那么∠BDE+∠AED的度数为( )
如图,△ABC中,∠C=60°,剪去这个60°角后,得到一个四边形,那么∠BDE+∠AED的度数为( )| A、180° | B、240° |
| C、120° | D、300° |
一次函数y=7x-3的图象不经过( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
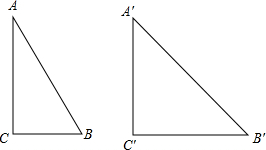 如图,在△ABC中,∠C=90°,∠A=30°.在△A′B′C′中,∠C′=90°,A′C′=B′C′.能否分别将这两个三角形各自分割成两个三角形,使△ABC所分成的两个三角形与△A′B′C′所分成的两个三角形分别对应相似?若能,请设计一种分割方案;若不能,请说明理由.
如图,在△ABC中,∠C=90°,∠A=30°.在△A′B′C′中,∠C′=90°,A′C′=B′C′.能否分别将这两个三角形各自分割成两个三角形,使△ABC所分成的两个三角形与△A′B′C′所分成的两个三角形分别对应相似?若能,请设计一种分割方案;若不能,请说明理由.