题目内容
16. 如图,在△ABC中,∠ACB=90°,斜边AB在x轴上,点C在y轴的正半轴上,直线AC的解析式是y=-2x+4,则直线BC的解析式为y=$\frac{1}{2}$x+4.
如图,在△ABC中,∠ACB=90°,斜边AB在x轴上,点C在y轴的正半轴上,直线AC的解析式是y=-2x+4,则直线BC的解析式为y=$\frac{1}{2}$x+4.
分析 先根据直线AC的解析式是y=-2x+4,求出A、C两点的坐标,得出OA、OC的长,再证明△BOC∽△COA,根据相似三角形对应边的比相等,得到B的坐标,最后根据待定系数法就可以求出直线BC的解析式.
解答 解:∵直线AC的解析式是y=-2x+4,
∴点A的坐标为(2,0),则OA=2,
点C的坐标为(0,4),则OC=4,
∵△BOC∽△COA,
∴$\frac{OB}{OC}$=$\frac{OC}{OA}$,
∴OB=$\frac{16}{2}$=8,
∴B的坐标是(-8,0).
设直线BC的解析式是y=kx+b,
则$\left\{\begin{array}{l}{-8k+b=0}\\{b=4}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{1}{2}}\\{b=4}\end{array}\right.$,
∴直线BC的解析式是y=$\frac{1}{2}$x+4.
故答案为y=$\frac{1}{2}$x+4.
点评 本题考查了待定系数法求一次函数的解析式,相似三角形的判定与性质,一次函数图象上点的坐标特征,求出B的坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下列函数中,正比例函数是( )
| A. | y=$\frac{2}{3x}$ | B. | y=$\frac{2}{3}$x-1 | C. | y=$\frac{3}{4}$x | D. | y=$\frac{1}{2}$(x-1) |
1.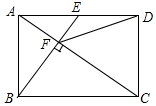 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )
 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=$\sqrt{2}$.四个结论中正确结论的概率是( )| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | 1 |
5.下列说法中正确的是( )
| A. | 8时45分,时针与分针的夹角是30° | B. | 6时30分,时针与分针重合 | ||
| C. | 3时30分,时针与分针的夹角是90° | D. | 9时整,时针与分针的夹角是90° |