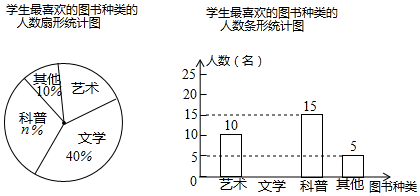
题目内容
6．下列实数：-$\frac{2}{3}$，0，2.9$\stackrel{•}{5}$，-3.1415926，$\frac{π}{2}$，$\sqrt{25}$，$\sqrt{3}$，0，0.020020002…中，无理数有（ ）个．| A． | 2 | B． | 3 | C． | 4 | D． | 5 |
分析 根据无理数、有理数的定义即可判定选择项．
解答 解：$\frac{π}{2}$，$\sqrt{3}$，0.020020002…是无理数，
故选：B．
点评 此题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．如π，$\sqrt{6}$，0.8080080008…（每两个8之间依次多1个0）等形式．
练习册系列答案
相关题目
如图，在△ABC中，∠ACB=90°，斜边AB在x轴上，点C在y轴的正半轴上，直线AC的解析式是y=-2x+4，则直线BC的解析式为y=$\frac{1}{2}$x+4．
14．
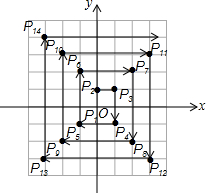如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长度，P1，P2，P3，…均在格点上，其顺序按图中“→”方向排列，如：P1（0，0），P2（0，1），P3（1，1），P4（1，-1），P5（-1，-1），P6（-1，2）…根据这个规律，点P2017的坐标为（ ）
如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长度，P1，P2，P3，…均在格点上，其顺序按图中“→”方向排列，如：P1（0，0），P2（0，1），P3（1，1），P4（1，-1），P5（-1，-1），P6（-1，2）…根据这个规律，点P2017的坐标为（ ）| A． | （-504，-504） | B． | （-505，-504） | C． | （504，-504） | D． | （-504，505） |
1．
如图，已知，点A（0，0）、B（4$\sqrt{3}$，0）、C（0，4），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第2017个等边三角形的边长等于（ ）
如图，已知，点A（0，0）、B（4$\sqrt{3}$，0）、C（0，4），在△ABC内依次作等边三角形，使一边在x轴上，另一个顶点在BC边上，作出的等边三角形分别是第1个△AA1B1，第2个△B1A2B2，第3个△B2A3B3，…则第2017个等边三角形的边长等于（ ）| A． | $\frac{\sqrt{3}}{{2}^{2015}}$ | B． | $\frac{\sqrt{3}}{{2}^{2016}}$ | C． | $\frac{\sqrt{3}}{{2}^{2017}}$ | D． | $\frac{\sqrt{3}}{{2}^{2019}}$ |
11．
如图所示，该几何体的左视图是（ ）
如图所示，该几何体的左视图是（ ）| A． |  | B． |  | C． |  | D． |  |
16．2017年，在创建文明城市的进程中，乌鲁木齐市为美化城市环境，计划种植树木30万棵，由于志愿者的加入，实际每天植树比原计划多20%，结果提前5天完成任务，设原计划每天植树x万棵，可列方程是（ ）
| A． | $\frac{30}{x}$-$\frac{30}{（1+20%）x}$=5 | B． | $\frac{30}{x}$-$\frac{30}{20%x}$=5 | C． | $\frac{30}{20%x}$+5=$\frac{30}{x}$ | D． | $\frac{30}{（1+20%）x}$-$\frac{30}{x}$=5 |