题目内容
5.下列二次根式中,不能与$\sqrt{3}$合并的是( )| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{8}$ | C. | $\sqrt{12}$ | D. | $\sqrt{27}$ |
分析 根据能合并二次根式,可得化简后的被开方数相同,可得答案.
解答 解:A、$\sqrt{\frac{1}{3}}=\frac{\sqrt{3}}{3}$,能与$\sqrt{3}$合并,故不合题意;
B、$\sqrt{8}=2\sqrt{2}$与$\sqrt{3}$不是同类二次根式,符合题意;
C、$\sqrt{12}=2\sqrt{3}$,能与$\sqrt{3}$合并,故不合题意;
D、$\sqrt{27}=3\sqrt{3}$,能与$\sqrt{3}$合并,故不合题意;
故选:B.
点评 本题考查了同类二次根式,化简后被开方数相同的二次根式是同类二次根式.

练习册系列答案
相关题目
15.一个长方形在平面直角坐标系中,它的三个顶点的坐标分别为(-3,-1),(2,-1),(2,2),则第四个顶点的坐标为( )
| A. | (-3,2) | B. | (3,2) | C. | (-3,-4) | D. | (7,2) |
16.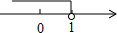 不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
 不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )
不等式ax-2<0的解集在数轴上表示如图,那么a的取值范围是( )| A. | a<1 | B. | a<2 | C. | a=1 | D. | a=2 |
20.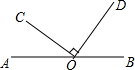 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
 如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )
如图,点O在直线AB上,且OC⊥OD,若∠DOB=46°,则∠COA的大小是( )| A. | 34° | B. | 44° | C. | 54° | D. | 64° |
15.下列说法中,正确的是( )
| A. | -$\frac{3}{4}$x2的系数是$\frac{3}{4}$ | B. | $\frac{3}{2}$πa2的系数是$\frac{3}{2}$ | C. | 3ab2的系数是3a | D. | $\frac{2}{5}$xy2的系数是$\frac{2}{5}$ |
 某经销商批发了一批无锡水蜜桃,为了打开销路,对1200个水蜜桃进行打包优惠出售,打包方式及售价如图,假设用这两种打包方式恰好装完全部水蜜桃.
某经销商批发了一批无锡水蜜桃,为了打开销路,对1200个水蜜桃进行打包优惠出售,打包方式及售价如图,假设用这两种打包方式恰好装完全部水蜜桃.