题目内容
在△ABC中，C、C′关于DE对称，判断∠1，∠2，∠C′的关系并证明．考点：轴对称的性质
专题：
分析：分别根据三角形内角和定理以及平角的定义，进而得出∠1+∠2=∠C+∠C′，再利用对称的性质求出即可．
解答：解：2∠C′=∠1+∠2．
理由：∵∠CDE+∠C′DE+∠C+∠C′+∠CDE+∠C′ED=360°，
∠CDE+∠EDC′+∠1+∠CDE+∠C′ED+∠2=360°，
∴∠1+∠2=∠C+∠C′，
∵在△ABC中，C、C′关于DE对称，
∴∠C=∠C′，
∴2∠C′=∠1+∠2．
理由：∵∠CDE+∠C′DE+∠C+∠C′+∠CDE+∠C′ED=360°，
∠CDE+∠EDC′+∠1+∠CDE+∠C′ED+∠2=360°，
∴∠1+∠2=∠C+∠C′，
∵在△ABC中，C、C′关于DE对称，
∴∠C=∠C′，
∴2∠C′=∠1+∠2．
点评：此题主要考查了三角形内角和定理以及平角的定义和对称的性质，得出∠1+∠2=∠C+∠C′是解题关键．
练习册系列答案
相关题目
本学期的五次数学单元练习中，甲、乙两位同学的平均成绩一样，方差分别为1.2，0.5，由此可知（ ）
| A、甲比乙的成绩稳定 |
| B、甲乙两人的成绩一样稳定 |
| C、乙比甲的成绩稳定 |
| D、无法确定谁的成绩更稳定 |
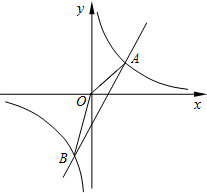如图，已知反比例函数y1=
如图，直角坐标系中，△ABC的顶点都在网格点上，其中C点坐标为（1，1），