题目内容
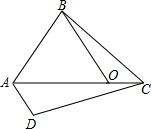 如图,△AOB为等边三角形,C为AO延长线上一定点,∠BCD=60°,CD与过A点且平行于OB的直线交于D.
如图,△AOB为等边三角形,C为AO延长线上一定点,∠BCD=60°,CD与过A点且平行于OB的直线交于D.(1)求∠OBC和∠ACD的关系;
(2)求证:CB=CD;
(3)求AC、AD、OA之间的关系.
考点:全等三角形的判定与性质
专题:
分析:认真阅读明确题意,抓住命题中给出的关键信息;
(1)较为简单,借助外角定理即可解决;
(2)(3)为探究线段之间的数量关系问题,常常借助全等三角形来解决.
(1)较为简单,借助外角定理即可解决;
(2)(3)为探究线段之间的数量关系问题,常常借助全等三角形来解决.
解答:(1)解:∠OBC=∠ACD,理由如下:
∵△AOB是等边三角形,∠BCD=60°,
∴∠BOA=∠BCD=60°.
∵∠BOA是△BOC的外角,
∴∠BOA=∠BCO+∠OBC=60°.
∵∠BCD=∠BCO+∠ACD=60°,
∴∠OBC=∠ACD;
(2)证明:如图: 连接BD.
连接BD.
由(1)知∠BAD=∠BAC+∠DAC=120°,
而∠BCD=60°,
∴∠BAD+∠BCD=180°,四边形ABCD四点共圆;
∴∠BDA=∠BCO;
∵∠BOC=180°-60°=120°,∠BAD=120°,
∴∠BAD=∠BOC;
∵AB=BC,
根据AAS定理,∴△BAD≌△BOC,
故CB=CD
(3)∵△BAD≌△BOC,
∴OC=AD;
∵AC=AO+OC,∴AC=AO+AD
∵△AOB是等边三角形,∠BCD=60°,
∴∠BOA=∠BCD=60°.
∵∠BOA是△BOC的外角,
∴∠BOA=∠BCO+∠OBC=60°.
∵∠BCD=∠BCO+∠ACD=60°,
∴∠OBC=∠ACD;
(2)证明:如图:
 连接BD.
连接BD.由(1)知∠BAD=∠BAC+∠DAC=120°,
而∠BCD=60°,
∴∠BAD+∠BCD=180°,四边形ABCD四点共圆;
∴∠BDA=∠BCO;
∵∠BOC=180°-60°=120°,∠BAD=120°,
∴∠BAD=∠BOC;
∵AB=BC,
根据AAS定理,∴△BAD≌△BOC,
故CB=CD
(3)∵△BAD≌△BOC,
∴OC=AD;
∵AC=AO+OC,∴AC=AO+AD
点评:该命题主要考查了全等三角形的判定及其性质的应用问题;三个小问题的设置由易到难、层层递进;对培养学生的探究能力提出了较高的要求;而作出辅助线,构造出一对全等等三角形又成为解题的关键.

练习册系列答案
相关题目
若甲数的
比乙数小1,乙数为2013,设甲数为x,则列方程为( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
方程2x(x-1)=x-1的解是( )
A、
| ||
B、-
| ||
C、
| ||
D、
|