题目内容
设m、n是一元二次方程x2+(p-2)x+1=0的两个根,且满足关系式[1+m(p+m)-n][1+n(p+n)-m]=-
,则p的值为 .
| 7 |
| 2 |
考点:根与系数的关系
专题:
分析:根据方程的解满足方程,把解代入方程,可得关于m、n的一元二次方程,根据根与系数的关系,可得m+n=2-p,mn=1,根据整式乘法,可得关于p的一元二次方程,根据解方程,可得答案.
解答:解:∵m、n 是一元二次方程 x2+(p-2)x+1=0 的两个根,
∴m2+(p-2)m+1=0,
∴m2+pm+1=2m,
同理n2+pn+1=2n.
由二次方程根与系数的关系,得
m+n=2-p,mn=1,
∴1+m(p+m)-n=1+mp+m2-n=2m-n,
同理得 1+n(p+n)-m=1+pn+n2-m=2n-m.
原式=(2m-n)(2n-m)=5mn-2m2-2n2=9mn-2(m+n)2=9-2(2-p)2=-
,
解得 p=
或p=-
.
∵方程有根,
∴△=(p-2)2-4≥0,
、-
均满足△≥0,
∴p=
或 p=-
,
故答案为:
,-
.
∴m2+(p-2)m+1=0,
∴m2+pm+1=2m,
同理n2+pn+1=2n.
由二次方程根与系数的关系,得
m+n=2-p,mn=1,
∴1+m(p+m)-n=1+mp+m2-n=2m-n,
同理得 1+n(p+n)-m=1+pn+n2-m=2n-m.
原式=(2m-n)(2n-m)=5mn-2m2-2n2=9mn-2(m+n)2=9-2(2-p)2=-
| 7 |
| 2 |
解得 p=
| 9 |
| 2 |
| 1 |
| 2 |
∵方程有根,
∴△=(p-2)2-4≥0,
| 9 |
| 2 |
| 1 |
| 2 |
∴p=
| 9 |
| 2 |
| 1 |
| 2 |
故答案为:
| 9 |
| 2 |
| 1 |
| 2 |
点评:本题考查了根与系数的关系,把解代入方程,可得关于m、n的一元二次方程是解题关键.

练习册系列答案
相关题目
某地在2007年工农业总产值10亿元,2008年增加了1.8亿元,其中工业增长率为24%,农业增长率为15%,则该地在2007年工农业生产值分别为( )亿元.
A、
| ||||
| B、3.3,6.7 | ||||
| C、4,7 | ||||
D、
|
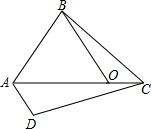 如图,△AOB为等边三角形,C为AO延长线上一定点,∠BCD=60°,CD与过A点且平行于OB的直线交于D.
如图,△AOB为等边三角形,C为AO延长线上一定点,∠BCD=60°,CD与过A点且平行于OB的直线交于D. 已知,如图所示,E是△ABC中线AD上一点,且BD2=ED•AD.求证:△ADC∽△CDE.
已知,如图所示,E是△ABC中线AD上一点,且BD2=ED•AD.求证:△ADC∽△CDE. 某公司共有50名员工,据初步统计,原来每人每年用于购买饮用瓶装矿泉水的支出约200元,经测算和市场调查,若该公司集体改饮“加林山”牌桶装矿泉水,则年费用由两部分组成:一部分是购买纯净水费用,另一部分为电费及购置饮水机等费用共约800元,其中矿泉水的销售价y与年购买总量x之间的关系如图所示:
某公司共有50名员工,据初步统计,原来每人每年用于购买饮用瓶装矿泉水的支出约200元,经测算和市场调查,若该公司集体改饮“加林山”牌桶装矿泉水,则年费用由两部分组成:一部分是购买纯净水费用,另一部分为电费及购置饮水机等费用共约800元,其中矿泉水的销售价y与年购买总量x之间的关系如图所示: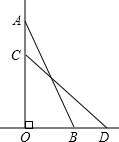 如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4m吗?
如图,一个25m长的梯子AB,斜靠在一竖直的墙AO上,这时的AO距离为24m,如果梯子的顶端A沿墙下滑4m,那么梯子底端B也外移4m吗?