题目内容
已知52m+1•53n-2=125，3m+5÷32n+5=
，试求m2+n-2的值．
| 1 |
| 81 |
考点：同底数幂的除法,同底数幂的乘法,解二元一次方程组
专题：计算题
分析：已知等式利用同底数幂的乘除法则变形，求出m与n的值，代入原式计算即可得到结果．
解答：解：52m+1•53n-2=52m+3n-1=125=53，3m+5÷32n+5=3m-2n=
=3-4，
可得
，
解得：m=-
，n=
，
则原式=
+
=
．
| 1 |
| 81 |
可得
|
解得：m=-
| 4 |
| 7 |
| 12 |
| 7 |
则原式=
| 16 |
| 49 |
| 49 |
| 144 |
| 4705 |
| 7056 |
点评：此题考查了同底数幂的除法，乘法，以及解二元一次方程组，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
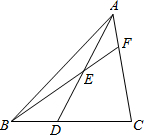如图，在△ABC中，D是BC上一点，E是AD的中点，BE的延长线交AC于点F，若
已知直线AB与反比例函数y=-已知y1=x+3，y2=6-x，当x=（ ）时，y1=2y2．
| A、1 | ||
| B、3 | ||
C、
| ||
D、
|