题目内容
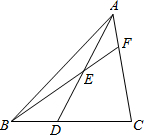 如图,在△ABC中,D是BC上一点,E是AD的中点,BE的延长线交AC于点F,若
如图,在△ABC中,D是BC上一点,E是AD的中点,BE的延长线交AC于点F,若| CD |
| DB |
| m |
| n |
| CF |
| FA |
考点:平行线分线段成比例,全等三角形的判定与性质
专题:
分析:过点E作EG∥AC,交BC于点G,则可知G为DC中点,则DC=2GC,且AC=2EG,利用
=
,可得到BD=
CG,则可求得
,可得到EG和CF的关系,从而可求得
.
| CD |
| DB |
| m |
| n |
| 2n |
| m |
| BD |
| BC |
| CF |
| FA |
解答: 解:过点E作EG∥AC,交BC于点G,
解:过点E作EG∥AC,交BC于点G,
∵E为AD中点,
∴G为DC中点,EG为△DAC的中位线,
∴DC=2CG,AC=2GE,
∵
=
,
∴
=
,
∴BD=
CG,
∴BC=BD+DC=
CG+2CG=
CG,
∴
=
=
=
=
,
∴CF=
EG,
∴AF=AC-CF=2EG-
EG=
EG,
∴
=
=
.
 解:过点E作EG∥AC,交BC于点G,
解:过点E作EG∥AC,交BC于点G,∵E为AD中点,
∴G为DC中点,EG为△DAC的中位线,
∴DC=2CG,AC=2GE,
∵
| CD |
| DB |
| m |
| n |
∴
| 2CG |
| BD |
| m |
| n |
∴BD=
| 2n |
| m |
∴BC=BD+DC=
| 2n |
| m |
| 2(m+n) |
| m |
∴
| EG |
| CF |
| BG |
| BC |
| BC-CG |
| BC |
| ||
|
| 2n+m |
| 2(m+n) |
∴CF=
| 2(m+n) |
| 2n+m |
∴AF=AC-CF=2EG-
| 2(m+n) |
| 2n+m |
| 2n |
| 2n+m |
∴
| CF |
| AF |
| ||
|
| m+n |
| n |
点评:本题主要考查平行线分线段成比例的性质,掌握平行线分线段对应成比例是解题关键,注意出现中点作平行线是常用的辅助线.

练习册系列答案
相关题目
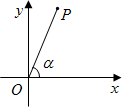 如图,在直角坐标系中,P是第一象限内的点,其坐标是(4,m),且OP与x轴正半轴的夹角α的余弦值是
如图,在直角坐标系中,P是第一象限内的点,其坐标是(4,m),且OP与x轴正半轴的夹角α的余弦值是| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图所示,已知AB∥A′B′,BC∥B′C′,求证:△OAC∽△OA′C′.
如图所示,已知AB∥A′B′,BC∥B′C′,求证:△OAC∽△OA′C′. 北宋末南宋初,中国象棋基本定型,开始风行全国.中国象棋规定:马走“日”(“
北宋末南宋初,中国象棋基本定型,开始风行全国.中国象棋规定:马走“日”(“ ”)字.现定义:在中国象棋的棋盘上,如图,从点A到点B,马走的最小步数称为A与B的马步距离.记作|AB|m,在图中画出了中国象棋的一部分,上面标有A,B,C,D,E共5个点,则在|AB|m、|AC|m、|AD|m、|AE|m中哪个最大?哪个最小?
”)字.现定义:在中国象棋的棋盘上,如图,从点A到点B,马走的最小步数称为A与B的马步距离.记作|AB|m,在图中画出了中国象棋的一部分,上面标有A,B,C,D,E共5个点,则在|AB|m、|AC|m、|AD|m、|AE|m中哪个最大?哪个最小?