题目内容
12.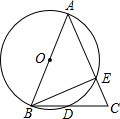 如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧$\widehat{AE}$是劣弧$\widehat{BD}$的2倍;⑤AE=BC,其中正确的序号是①②④.
如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下五个结论:①∠EBC=22.5°;②BD=DC;③AE=2EC;④劣弧$\widehat{AE}$是劣弧$\widehat{BD}$的2倍;⑤AE=BC,其中正确的序号是①②④.
分析 根据圆周角定理,等边对等角,等腰三角形的性质,直径对的圆周角是直角等知识,运用排除法逐条分析判断.
解答 解:连接AD,AB是直径,
则AD⊥BC,
又∵△ABC是等腰三角形,
故点D是BC的中点,即BD=CD,故②正确;
∵AD是∠BAC的平分线,
由圆周角定理知,∠EBC=∠DAC=$\frac{1}{2}$∠BAC=22.5°,故①正确;
∵∠ABE=90°-∠EBC-∠BAD=45°=2∠CAD,故④正确;
∵∠EBC=22.5°,2EC≠BE,AE=BE,∴AE≠2CE,③不正确;
∵AE=BE,BE是直角边,BC是斜边,肯定不等,故⑤错误.
综上所述,正确的结论是:①②④.
故答案是:①②④.
点评 本题考查了圆周角定理,等腰三角形的判定与性质以及弧长的计算等.利用了圆周角定理,等边对等角,等腰三角形的性质,直径对的圆周角是直角求解.

练习册系列答案
相关题目
2.如图,观察图形,找出规律,确定第四个图形是( )


| A. |  | B. |  | C. |  | D. |  |
3.不等式组$\left\{\begin{array}{l}{x+2a>4}\\{2x-b<5}\end{array}\right.$的解集是0<x<2,那么a+b=( )
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
7.不等式组$\left\{\begin{array}{l}{2x-3<4x+1}\\{\frac{1}{3}(x+3)≤2}\end{array}\right.$的解集在数轴上表示正确的是( )
| A. |  | B. |  | ||
| C. |  | D. |  |
 如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2
如图所示,矩形的长是4cm,宽是3cm,如果将其长与宽都增加x cm,那么面积增加y cm2 如图,在△ABC中,∠C>∠B,AD是△ABC的角平分线,AE⊥BC于点E,试说明∠DAE=$\frac{1}{2}$(∠C-∠B).
如图,在△ABC中,∠C>∠B,AD是△ABC的角平分线,AE⊥BC于点E,试说明∠DAE=$\frac{1}{2}$(∠C-∠B).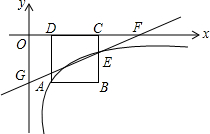 如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).
如图,正方形ABCD的顶点C,D在x轴的正半轴上,反比例函数y=$\frac{k}{x}$(k≠0)在第四象限的图象经过顶点A(m,-2)和BC边上的点E(n,-$\frac{2}{3}$),过点E的直线l交x轴于点F,交y轴于点G(0,-2),则点F的坐标是($\frac{9}{2}$,0).