题目内容
足球世界杯比赛分成8个小组,每个小组4个队,小组内进行单循环比赛(每个队都与该小组的其他队比赛一场),选出2个队进入16强.比赛规定胜一场得3分,平一场得1分,负一场得0分.请问:
(1)每个小组共比赛多少场?
(2)在小组比赛中,有一个队比赛结束后积分为6分,该队出线这一事件是什么事件?
(1)共比赛6场；(2)随机事件.
【解析】试题分析：对于（1），每个小组有4个队，每队要和其余的3个队进行比赛，故要比赛（4×3）场，而每两队之间只比赛一场，因此再除以2可完成解答；
对于（2），结合（1）的结论，先求出每组的最高得分，再求出剩下的分数，然后结合确定事件和随机事件的概念进行判断，即可完成解答.
【解析】
（1）(4×3) ÷2=6（场），
故每个小组...
53随堂测系列答案如图，△ABE和△ADC是△ABC分别沿AB、AC边翻折得到的，若∠1: ∠2:∠3 = 28 :5 : 3， 则∠4的度数为__________
80°
【解析】根据翻折求出各个角的度数，再根据三角形的一个外角等于和它不相邻的两个内角的和求出∠4的度数.
【解析】
∵∠1: ∠2:∠3 = 28 :5 : 3，
∠1+∠2+∠3 = 180°，
∴∠1=140°，∠2=25°，∠3=15°，
由翻折得∠EBA =∠2 =25°，∠DCA =∠3 =15°，
∴∠EBC=∠EBA +∠2 =50°，∠DC... 下列说法错误的是( )
A. 等边三角形是轴对称图形
B. 轴对称图形的对应边相等,对应角相等
C. 成轴对称的两条线段必在对称轴一侧
D. 成轴对称的两个图形对应点的连线被对称轴垂直平分
C
【解析】A. 由等边三角形的性质知,等边三角形是轴对称图形,正确;
B. 由轴对称的性质知,轴对称图形的对应边相等,对应角相等,正确;
C. 成轴对称的两条线段必在对称轴两侧,故错误;
D. 由轴对称的性质知,成轴对称的两个图形对应点的连线被对称轴垂直平分,正确;
故选C. 在下列条件中，不能确定四边形ABCD为平行四边形的是（ ）
A. ∠A=∠C，∠B=∠D B. ∠A=∠B=∠C=90°
C. ∠A+∠B=180°，∠B+∠C=180° D. ∠A+∠B=180°，∠C+∠D=180°
D
【解析】试题分析：A．∠A=∠C，∠B=∠D，能判定四边形ABCD是平行四边形；
B．∠A=∠B=∠C=90°，能判定四边形ABCD是平行四边形；
C．∠A+∠B=180°，∠B+∠C=180°，能判定四边形ABCD是平行四边形；
D．∠A+∠B=180°，∠C+∠D=180°，不能判定四边形ABCD是平行四边形．
故选D． 已知四边形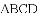
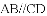
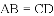
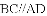
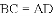
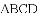
A. 6种 B. 5种 C. 4种 D. 3种
C
【解析】平行四边形的判定，平行四边形的判定方法共有五种，在四边形中如果有：
1、四边形的两组对边分别平行；
2、一组对边平行且相等；
3、两组对边分别相等；
4、对角线互相平分；
5、两组对角分别相等．则四边形是平行四边形
根据平行四边形的判定，符合条件的有4种，分别是：①②、③④、②③、①④．
故选C 小明投掷一枚质地均匀的骰子,前三次投出的朝上的数字都是6,则第4次投出的朝上的数字( )
A. 按照小明的运气来看,一定还是6
B. 前三次已经是6了,这次一定不是6
C. 按照小明的运气来看,是6的可能性最大
D. 是6的可能性与是1~5中任意一个数字的可能性相同
D
【解析】要求可能性的大小，只需求出各自所占的比例大小即可．
【解析】
一枚普通的骰子共有1、2、3、4、5、6六个数字，每一个数字朝上的可能性都相等，
所以第4次投出的朝上数字是6的可能性与是1～5中任意一个数字的可能性相同．
故选D． 下列事件中,是必然事件的是( )
A. 两条线段可以组成一个三角形
B. 400人中有两个人的生日在同一天
C. 早上的太阳从西方升起
D. 打开电视机,它正在播放动画片
B
【解析】试题解析：A. 两条线段可以组成一个三角形是不可能事件，故错误；
B.400人中有两个人的生日在同一天是必然事件，故正确；
C. 早上的太阳从西方升起是不可能事件，故错误；
D. 打开电视机，它正在播放动画片是随机事件，故错误；
故选B. 计算：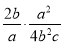 
＝________
【解析】试题解析：
故答案为： 两人比赛读一本科普读物共98页，王力读了一周（7天）还没有读完，而张勇不到一周就读完了．张勇平均每天比王力多读3页，王力平均每天读__页．（答案取整数）
12或13
【解析】【解析】
设王力平均每天读x页，则张勇平均每天读（x+3）页．根据题意得：
，解得：11＜x＜14．
∵x取整数，∴x=12或x=13．
故答案为：12或13．