题目内容
4. 如图,四边形ABCD中,∠ABC=∠ADC=90°,E、F分别是AC、BD的中点,∠BAC=15°,∠DAC=45°,则$\frac{EF}{CD}$的值为$\frac{\sqrt{2}}{4}$.
如图,四边形ABCD中,∠ABC=∠ADC=90°,E、F分别是AC、BD的中点,∠BAC=15°,∠DAC=45°,则$\frac{EF}{CD}$的值为$\frac{\sqrt{2}}{4}$.
分析 连接BE,ED,根据∠ABC=∠ADC=90°且E为AC中点,求证△BED是等腰三角形,再利用等腰三角形的高,中线,角平分线三线合一的性质得到EF⊥BD,
根据圆周角定理得到∠DEF=60°,求得EF=$\frac{1}{2}$DE,CD=$\sqrt{2}$DE,于是得出结论.
解答 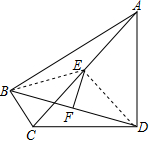 解:连接BE,ED,
解:连接BE,ED,
∵∠ABC=∠ADC=90°且E为AC中点,
∴DE=$\frac{1}{2}$AC,BE=$\frac{1}{2}$AC,
∴BE=DE,
∵F为BD中点,
∴EF⊥BD,
∵∠ABC=∠ADC=90°,
∴A,B,C,D四点共圆,
∵∠BAC=15°,∠DAC=45°,
∴∠BAD=60°,
∴∠BED=120°,
∴∠FED=60°,
∴EF=$\frac{1}{2}$DE,
∵CD=$\sqrt{2}$DE,
∴$\frac{EF}{CD}$=$\frac{\sqrt{2}}{4}$.
故答案为:$\frac{\sqrt{2}}{4}$.
点评 此题主要考查直角三角形斜边上的中线等于斜边的一半和等腰三角形的性质等知识点,解答此题的关键是连接BE,ED,根据∠ABC=∠ADC=90°且E为AC中点,证出△BED是等腰三角形.

练习册系列答案
相关题目
16.若角α、β是直角三角形的两个锐角,则$\frac{sinα}{cosβ}$-tan$\frac{α+β}{2}$的值为( )
| A. | 0 | B. | 1 | C. | 1-$\sqrt{2}$ | D. | $\frac{\sqrt{2}}{2}$-1 |
13. 二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
 二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )
二次函数y=ax2+bx+c的图象如图所示(a、b、c为常数),则函数y=(4ac-b2)x+abc和y=$\frac{2a+b}{x}$在同一平面直角坐标系中的图象,可能是( )| A. |  | B. |  | C. |  | D. |  |
14.下列运算正确的是( )
| A. | 3x+3y=6xy | B. | -y2-y2=0 | C. | 3(x+8)=3x+8 | D. | -(6x+2y)=-6x-2y |
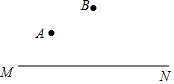 A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.
A、B两厂在公路MN同侧,拟在公路边建一货场C,若由B厂独家兴建,并考虑B厂的利益,则要求货场离B厂最近,请在图中作出此时货场C的位置,并说出这样做的道理.