题目内容
如图,在△ABC中,AB=AC,∠ABC和∠ACB的平分线交于点O.
(1)过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并判断EF、BE、FC之间的关系,并证明你的结论;
(2)若AB≠AC,其他条件不变,图中还有等腰三角形吗?若有,请写出所有的等腰三角形,若没有,请说明理由;线段EF、BE、FC之间,上面探究的结论是否还成立?

(1)过O作EF∥BC交AB于E,交AC于F.请你写出图中所有等腰三角形,并判断EF、BE、FC之间的关系,并证明你的结论;
(2)若AB≠AC,其他条件不变,图中还有等腰三角形吗?若有,请写出所有的等腰三角形,若没有,请说明理由;线段EF、BE、FC之间,上面探究的结论是否还成立?
考点:等腰三角形的判定与性质,平行线的性质
专题:
分析:(1)根据等腰三角形的判定,可得等腰三角形,根据角平分线的性质,可得∠EBO与CBO,∠FOC与∠FCO的关系,根据平行线的性质,可得∠EOB与∠CBO,∠FOC与∠BCO的关系,根据等腰三角形的判定,可得BE与EO,CF与FO的关系,根据线段的和差,可得答案;
(2)根据等腰三角形的判定,可得等腰三角形,根据角平分线的性质,可得∠EBO与CBO,∠FOC与∠FCO的关系,根据平行线的性质,可得∠EOB与∠CBO,∠FOC与∠BCO的关系,根据等腰三角形的判定,可得BE与EO,CF与FO的关系,根据线段的和差,可得答案.
(2)根据等腰三角形的判定,可得等腰三角形,根据角平分线的性质,可得∠EBO与CBO,∠FOC与∠FCO的关系,根据平行线的性质,可得∠EOB与∠CBO,∠FOC与∠BCO的关系,根据等腰三角形的判定,可得BE与EO,CF与FO的关系,根据线段的和差,可得答案.
解答:解:如图(1):
 ,
,
等腰三角形有:等腰△ABC,等腰△BEO,等腰△CFO,等腰△BOC,等腰△AEF,BE+CF=EF,理由如下:
∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠FOC=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO.
∵EO+OF=EF,
∴BE+CF=EF;
(2)如图(2):

有等腰三角形,BE+CF=EF仍成立,
等腰△BEO,等腰△CFO,
理由如下:
∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠FOC=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO.
∵EO+OF=EF,
∴BE+CF=EF.
 ,
,等腰三角形有:等腰△ABC,等腰△BEO,等腰△CFO,等腰△BOC,等腰△AEF,BE+CF=EF,理由如下:
∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠FOC=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO.
∵EO+OF=EF,
∴BE+CF=EF;
(2)如图(2):

有等腰三角形,BE+CF=EF仍成立,
等腰△BEO,等腰△CFO,
理由如下:
∵BO平分∠ABC,CO平分∠ACB,
∴∠EBO=CBO,∠FOC=∠FCO.
∵EF∥BC,
∴∠EOB=∠CBO,∠FOC=∠BCO,
∴∠EBO=∠EOB,∠FOC=∠FCO,
∴BE=EO,CF=FO.
∵EO+OF=EF,
∴BE+CF=EF.
点评:本题考查了等腰三角形的判定与性质,利用了等腰三角形的判定与性质,角平分线的性质,平行线的性质.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
某大米包装袋上标注着“净含量10㎏±150g”,小华从商店买了2袋大米,这两袋大米相差的克数不可能是( )
| A、100g | B、150g |
| C、300g | D、400g |
 如图,已知在圆内接四边形ABCD中,∠CAD=∠CAB=60°,求证:△BDC是等边三角形.
如图,已知在圆内接四边形ABCD中,∠CAD=∠CAB=60°,求证:△BDC是等边三角形.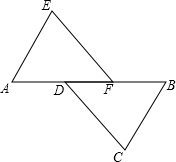 如图,A、D、F、B在同一直线上,AD=BF,EF=CD,且EF∥CD.
如图,A、D、F、B在同一直线上,AD=BF,EF=CD,且EF∥CD.