题目内容
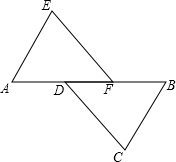如图，A、D、F、B在同一直线上，AD=BF，EF=CD，且EF∥CD．求证：（1）△AEF≌△BCD；
（2）AE∥BC．
考点：全等三角形的判定与性质,平行线的判定
专题：证明题
分析：（1）由平行可得∠EFA=∠CDB，由AD=BF可得AF=BD，结合EF=CD，则可证明△AEF≌△BCD；
（2）利用（1）中的结论可得∠A=∠B，可得AE∥BC．
（2）利用（1）中的结论可得∠A=∠B，可得AE∥BC．
解答：证明：（1）∵EF∥CD，
∴∠EFA=∠CDB，
∵AD=BF，
∴AD+DF=DF+FB，即AF=BD，
在△AEF和△BCD中，
，
∴△AEF≌△BCD（SAS）；
（2）由（1）可得△AEF≌△BCD，
∴∠A=∠B，
∴AE∥BC．
∴∠EFA=∠CDB，
∵AD=BF，
∴AD+DF=DF+FB，即AF=BD，
在△AEF和△BCD中，
|
∴△AEF≌△BCD（SAS）；
（2）由（1）可得△AEF≌△BCD，
∴∠A=∠B，
∴AE∥BC．
点评：本题主要考查全等三角形的判定和性质，掌握全等三角形的判定方法是解题的关键，三角形全等的判定方法有SSS、SAS、ASA、AAS和HL．
练习册系列答案
春雨教育同步作文系列答案
相关题目
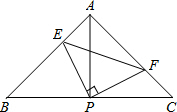如图，已知△ABC中，AB=AC，∠BAC=90°，直角∠EPF的顶点P是BC中点，两边PE、PF分别交AB、AC于点E、F，给出以下四个结论：①AE=CF； ②△EPF是等腰直角三角形； ③S四边形AEPF=
已知：如图，点C为线段AB上的一点，△ACM和△CBN是等边三角形，直线AN、CM交于点E，直线BM、CN交于点F．