题目内容
3.计算:(1)$\frac{x+2}{x+1}-\frac{x+3}{x+2}+\frac{x-5}{x-4}-\frac{x-4}{x-3}$
(2)$\frac{1}{x(x+2)}$+$\frac{1}{(x+2)(x+4)}$.
分析 (1)原式变形后,通分并利用同分母分式的加减法则计算即可得到结果;
(2)原式通分并利用同分母分式的加法法则计算即可得到结果.
解答 解:(1)原式=1+$\frac{1}{x+1}$-1-$\frac{1}{x+2}$+1-$\frac{1}{x-4}$-1+$\frac{1}{x-3}$=$\frac{x+2-x-1}{(x+1)(x+2)}$+$\frac{x-4-x+3}{(x-3)(x-4)}$=$\frac{1}{(x+1)(x+2)}$-$\frac{1}{(x-3)(x-4)}$=$\frac{{x}^{2}-7x+12-{x}^{2}-3x-2}{(x+1)(x+2)(x-3)(x-4)}$=$\frac{-10(x-1)}{(x+1)(x+2)(x-3)(x-4)}$;
(2)原式=$\frac{x+4}{x(x+2)(x+4)}$+$\frac{x}{x(x+2)(x+4)}$=$\frac{2(x+2)}{x(x+2)(x+4)}$=$\frac{2}{x(x+4)}$.
点评 此题考查了分式的加减法,熟练掌握运算法则是解本题的关键.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目
1.在平面直角坐标系中,将点A(-2,1)向左平移2个单位,再向上平移3个单位到点Q,则点Q的坐标为( )
| A. | (-2,3) | B. | (0,-2) | C. | (-4,4) | D. | (-4,-2) |
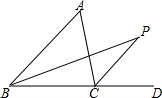 如图,△ABC的外角∠ACD的平分线与内角∠ABC平分线交于点P,若∠BPC=25°,则∠BAC的度数是50°.
如图,△ABC的外角∠ACD的平分线与内角∠ABC平分线交于点P,若∠BPC=25°,则∠BAC的度数是50°.