题目内容
11.解方程组:$\left\{\begin{array}{l}{x-9y=-9}\\{y-z=3}\\{2z+x=47}\end{array}\right.$.分析 由③-①得出y和z的方程,与②联立解关于y,z的方程,再进一步求得z的数值解决问题.
解答 解:$\left\{\begin{array}{l}{x-9y=-9①}\\{y-z=3②}\\{2z+x=47③}\end{array}\right.$,
③-①得:2z+9y=56④;
联立②④方程可得:$\left\{\begin{array}{l}{2z+9y=56④}\\{y-z=3②}\end{array}\right.$,
把②代入④得:z=$\frac{29}{11}$,
把z=$\frac{29}{11}$代入②得:y=$\frac{62}{11}$,
把y=$\frac{62}{11}$代入①得:x=$\frac{459}{11}$,
所以方程组的解是:$\left\{\begin{array}{l}{x=\frac{459}{11}}\\{y=\frac{62}{11}}\\{z=\frac{29}{11}}\end{array}\right.$
点评 此题考查三元一次方程组的解法,注意逐步消元是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.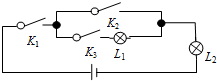 物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
 物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )
物理某一实验的电路图如图所示,其中K1,K2,K3 为电路开关,L1,L2为能正常发光的灯泡.任意闭合开关K1,K2,K3中的两个,那么能让两盏灯泡同时发光的概率为( )| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |
8.找出以下图形变化的规律,则第2015个图形中黑色正方形的数量是( )


| A. | 3020 | B. | 3021 | C. | 3022 | D. | 3023 |