题目内容
7.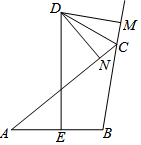 已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的长.
已知,如图,DE为△ABC的边AB的垂直平分线,CD为△ABC的外角平分线,与DE交于D,DM⊥BC于M,DN⊥AC于N,若CM=1,BC=3,求AN的长.
分析 连接AD、DB.首先证明DA=DB,DM=DN,再证明Rt△ADN≌Rt△BDM即可解决问题.
解答 解:连接AD、DB.
∵DE垂直平分线段AB,
∴DA=DB,
∵CD平分∠MCN,DM⊥CM,DN⊥CN,
∴DN=DM,∠AND=∠DMB=90°,
在Rt△ADN和Rt△BDM中,
$\left\{\begin{array}{l}{AD=BD}\\{DN=DM}\end{array}\right.$,
∴Rt△ADN≌Rt△BDM,
∴AN=BM,
∵BM=BC+CM=4,
∴AN=4.
点评 本题考查线段的垂直平分线的性质,角平分线的性质定理、全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
17.一次函数y=2x-1与反比例函数y=-$\frac{1}{x}$的图象的交点的情况为( )
| A. | 只有一个交点 | B. | 有两个交点 | C. | 没有交点 | D. | 不能确定 |
14. 如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )
如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )
 如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )
如图,⊙O的半径为2,AB,CD是两条互相垂直的直径,点P是⊙O上任意一点(点P与点A,B,C,D均不重合),过点P作PM⊥AB于点M.PN⊥CD于点N,点Q是线段MN的中点.若点P以点O为旋转中心.沿着圆周顺时针旋转45°.则点Q经过的路径长为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{3}$ |
2.据《楚天都市报》消息,武汉市居民生活用水价格将进行自1999年以来的第四次调整,试行居民生活用水阶梯式计量水价.拟定城市居民用水户每月用水量在22立方米以内的,为第一级基数,按调整后的居民生活用水价格收取;超过22立方米且低于30立方米(含30立方米)的部分为第二级水量基数,按调整后价格的1.5倍收取;超过30立方米的部分为第三级水量基数,按调整后价格的2倍收取.
为了节约用水,小杜记录了2013年1月-7月份他家每月1号水表的读数及所交水款.
(1)求小杜家1-6月平均每月用水量;
(2)调整后的第一级基数,第二级基数,第三级基数的水费分别是每立方米多少钱?
(3)若下半年比上半年少用水10%,则下半年的水费大约为多少元?
(4)若恬恬家12月份交的水费为66.44元,恬恬家12月份用水多少立方米?
为了节约用水,小杜记录了2013年1月-7月份他家每月1号水表的读数及所交水款.
| 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | |
| 水表止码(单位:立方米) | 2234 | 2244 | 2253 | 2262 | 2273 | 2283 | 2294 |
| 水费(单位:元) | 24.16 | 15.10 | 13.59 | 13.59 | 16.61 | 15.10 | 16.61 |
(2)调整后的第一级基数,第二级基数,第三级基数的水费分别是每立方米多少钱?
(3)若下半年比上半年少用水10%,则下半年的水费大约为多少元?
(4)若恬恬家12月份交的水费为66.44元,恬恬家12月份用水多少立方米?
17. 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠CBA的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠CBA的度数为( )
 如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠CBA的度数为( )
如图,AB是⊙O的切线,B为切点,AO与⊙O交于点C,若∠BAO=40°,则∠CBA的度数为( )| A. | 15° | B. | 20° | C. | 25° | D. | 30° |
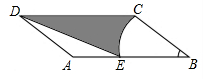 如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BG为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π.(结果保留π)
如图,在平行四边形ABCD中,AB=5,AD=2,∠B=60°,以点B为圆心,BG为半径的圆弧交AB于点E,连接DE,则图中阴影部分的面积为$\frac{7\sqrt{3}}{2}$-$\frac{2}{3}$π.(结果保留π)