题目内容
2．已知△ABC∽△DEF，S△ABC：S△DEF=1：4．若BC=1，则EF的长为（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
分析 根据相似三角形的面积的比等于相似比的平方求得相似比后即可求得线段EF的长．
解答 解：∵△ABC∽△DEF，S△ABC：S△DEF=1：4，
∴BC：EF=1：2，
∵BC=1，
∴EF=2，
故选B．
点评 此题考查了相似三角形的性质，解题的关键是了解相似三角形的面积的比等于相似比的平方，难度不大．
练习册系列答案
名校课堂系列答案
相关题目
12．
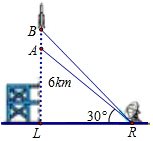如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于地面R处的雷达站观测得知AR的距离是6km，仰角∠ARL=30°，又经过1s后火箭到达B点，此时测得仰角∠BRL=45°，则这枚火箭从A到B的平均速度为（ ）km/s．
如图，一枚运载火箭从地面L处发射，当火箭到达A点时，从位于地面R处的雷达站观测得知AR的距离是6km，仰角∠ARL=30°，又经过1s后火箭到达B点，此时测得仰角∠BRL=45°，则这枚火箭从A到B的平均速度为（ ）km/s．| A． | 3$\sqrt{3}$-3 | B． | 3$\sqrt{3}$ | C． | 3$\sqrt{3}$+3 | D． | 3 |
17．一次函数y=2x-1与反比例函数y=-$\frac{1}{x}$的图象的交点的情况为（ ）
| A． | 只有一个交点 | B． | 有两个交点 | C． | 没有交点 | D． | 不能确定 |
7．如图，将正方形ABCD的四个角向内折起，恰好拼成一个无缝无重叠的四边形EFGH，再将四边形EFGH的一个角向内折起，使点F恰好和EG的中点重合，折痕为IJ，若点H到IJ的距离HK=9cm，则边AB的长是（ ）
| A． | 16cm | B． | 12cm | C． | 9cm | D． | 6$\sqrt{2}$cm |
14．
如图，⊙O的半径为2，AB，CD是两条互相垂直的直径，点P是⊙O上任意一点（点P与点A，B，C，D均不重合），过点P作PM⊥AB于点M．PN⊥CD于点N，点Q是线段MN的中点．若点P以点O为旋转中心．沿着圆周顺时针旋转45°．则点Q经过的路径长为（ ）
如图，⊙O的半径为2，AB，CD是两条互相垂直的直径，点P是⊙O上任意一点（点P与点A，B，C，D均不重合），过点P作PM⊥AB于点M．PN⊥CD于点N，点Q是线段MN的中点．若点P以点O为旋转中心．沿着圆周顺时针旋转45°．则点Q经过的路径长为（ ）| A． | $\frac{π}{4}$ | B． | $\frac{π}{2}$ | C． | $\frac{π}{6}$ | D． | $\frac{π}{3}$ |