题目内容
19.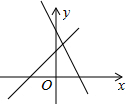 如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )
如图,一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)在同一坐标系的图象.则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中( )| A. | m>0,n>0 | B. | m>0,n<0 | C. | m<0,n>0 | D. | m<0,n<0 |
分析 方程组$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解就是一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)图象的交点,根据交点所在象限确定m、n的取值范围.
解答 解:方程组$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解就是一次函数y1=ax+b和y2=-bx+a(a≠0,b≠0)图象的交点,
∵两函数图象交点在第一象限,
∴m>0,n>0,
故选:A.
点评 此题主要考查了一次函数与二元一次方程组的解,关键是掌握两函数图象的交点就是两函数解析式组成的方程组的解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.点M(3,1)关于x轴对称的点的坐标为( )
| A. | (-3,-1) | B. | (-3,1) | C. | (1,-3) | D. | (3,-1) |
7.下列说法中正确的个数是( )
①“对顶角相等”的逆命题是真命题.
②数据3,5,4,2,-1的中位数是3.
③正比例函数y=kx(k≠0)的图象经过点(0,0)和(1,k).
④无限小数都是无理数.
①“对顶角相等”的逆命题是真命题.
②数据3,5,4,2,-1的中位数是3.
③正比例函数y=kx(k≠0)的图象经过点(0,0)和(1,k).
④无限小数都是无理数.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.下列运算中,正确的是( )
| A. | 4a•3a=12a | B. | (ab2)2=ab4 | C. | (3a2)3=9a6 | D. | a•a2=a3 |
9.若-$\sqrt{5}$$<x<\sqrt{3}$,且x是整数,则满足条件的x值有( )
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
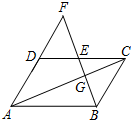 如图,?ABCD中,E是边CD的中点,连结BE并延长,交AD的延长线于点F.
如图,?ABCD中,E是边CD的中点,连结BE并延长,交AD的延长线于点F.