题目内容
4．3点30分，时针与分针所形成的夹角等于75°．分析 根据时针与分针相距的份数乘以每份的度数，可得答案．
解答 解：3点30分时针与分针相距2+$\frac{30}{60}$=$\frac{5}{2}$份，
3点30分时针与分针所形成的夹角等于30×$\frac{5}{2}$=75°，
故答案为：75．
点评 本题考查了钟面角，利用时针与分针相距的份数乘以每份的度数是解题关键．
练习册系列答案
相关题目
14．已知cosB=$\frac{{\sqrt{3}}}{2}$，则∠B的值为（ ）
| A． | 30° | B． | 60° | C． | 45° | D． | 90° |
如图，直角三角形斜边长为12，内切圆的半径为1，求三角形的周长．
12．-2016的相反数是（ ）
| A． | $-\frac{1}{2016}$ | B． | $\frac{1}{2016}$ | C． | 6102 | D． | 2016 |
19．
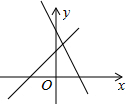如图，一次函数y1=ax+b和y2=-bx+a（a≠0，b≠0）在同一坐标系的图象．则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中（ ）
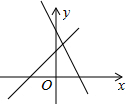如图，一次函数y1=ax+b和y2=-bx+a（a≠0，b≠0）在同一坐标系的图象．则$\left\{\begin{array}{l}{y_1}=ax+b\\{y_2}=-bx+a\end{array}\right.$的解$\left\{\begin{array}{l}x=m\\ y=n\end{array}\right.$中（ ）| A． | m＞0，n＞0 | B． | m＞0，n＜0 | C． | m＜0，n＞0 | D． | m＜0，n＜0 |
16．某工厂计划生产A、B两种产品共10件，其生产成本和利润如下表：
（1）若工厂计划获利14万元，问A、B两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于35万元，且获利多于14万元，问工厂有哪几种生产方案？
（3）在（2）的条件下，哪种生产方案获利最大？并求出最大利润．
| A种产品 | B种产品 | |
| 成本（万元/件） | 2 | 5 |
| 利润（万元/件） | 1 | 3 |
（2）若工厂计划投入资金不多于35万元，且获利多于14万元，问工厂有哪几种生产方案？
（3）在（2）的条件下，哪种生产方案获利最大？并求出最大利润．
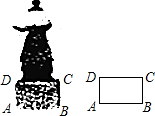如图，广场上雕塑底座正面ABCD是一个四边形且边AB=40cm，小明想要检测雕塑底座的AD是否垂直于底边AB，但他随身只带有一个长度为20cm的刻度尺和计算工具，他能有办法检验边AD是否垂直于边AB吗？请你帮小明设计一个可行的方案．