题目内容
5.设方程x2+x-2=0的两个根为α,β,那么(α-1)(β-1)的值等于0.分析 根据方程的系数利用根与系数的关系找出α+β=-1、α•β=-2,将(α-1)(β-1)展开后代入数据即可得出结论.
解答 解:∵方程x2+x-2=0的两个根为α,β,
∴α+β=-1,α•β=-2,
∴(α-1)(β-1)=α•β-(α+β)+1=-2-(-1)+1=0.
故答案为:0.
点评 本题考查了根与系数的关系,解题的关键是根据根与系数的关系找出α+β=-1、α•β=-2.本题属于基础题,难度不大,解决该题型题目时,根据方程的系数结合根与系数的关系找出两根之和与两根之积是关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
10.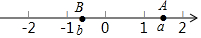 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
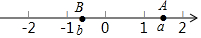 如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )
如图,A,B两点在数轴上表示的数分别是a,b,下列式子成立的是( )| A. | ab>0 | B. | b-a>0 | C. | (a-1)(b-1)>0 | D. | (a-1)(b+1)>0 |
17.在有理数(-1)2、-(-$\frac{3}{2}$)、|-2|中负数有( )个.
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
 如图所示,A、B两点的坐标分别是A(1,$\sqrt{2}$),B($\sqrt{5}$,0),如果把A、B两点的纵、横坐标都同时扩大2倍.
如图所示,A、B两点的坐标分别是A(1,$\sqrt{2}$),B($\sqrt{5}$,0),如果把A、B两点的纵、横坐标都同时扩大2倍. 抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点是点A(3,0),其部分图象如图,则下列结论:
抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点是点A(3,0),其部分图象如图,则下列结论: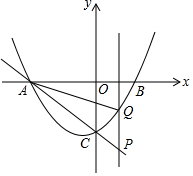 已知抛物线y=$\frac{1}{4}$x2+$\frac{1}{4}$x-3交x轴于A,B两点,交y轴于点C,点P是直线AC上的一个动点,过点P作PQ⊥x轴,交抛物线于点Q,连结CQ.设点P的横坐标为m.
已知抛物线y=$\frac{1}{4}$x2+$\frac{1}{4}$x-3交x轴于A,B两点,交y轴于点C,点P是直线AC上的一个动点,过点P作PQ⊥x轴,交抛物线于点Q,连结CQ.设点P的横坐标为m.