题目内容
16. 如图所示,A、B两点的坐标分别是A(1,$\sqrt{2}$),B($\sqrt{5}$,0),如果把A、B两点的纵、横坐标都同时扩大2倍.
如图所示,A、B两点的坐标分别是A(1,$\sqrt{2}$),B($\sqrt{5}$,0),如果把A、B两点的纵、横坐标都同时扩大2倍.(1)求扩大后,点A、B的对应点D、E的坐标;
(2)△ODE的面积是多少?
分析 (1)直接写出D、E的坐标;
(2)作高DF,根据坐标得:DF=2$\sqrt{2}$,OE=2$\sqrt{5}$,代入面积公式计算即可.
解答 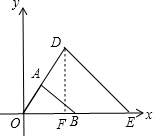 解:(1)D(2,2$\sqrt{2}$),E(2$\sqrt{5}$,0);
解:(1)D(2,2$\sqrt{2}$),E(2$\sqrt{5}$,0);
(2)如图,过D作DF⊥x轴于F,
∵D(2,2$\sqrt{2}$),E(2$\sqrt{5}$,0),
∴DF=2$\sqrt{2}$,OE=2$\sqrt{5}$,
∴△ODE的面积=$\frac{1}{2}$OE•DF=$\frac{1}{2}$×2$\sqrt{5}$×2$\sqrt{2}$=2$\sqrt{10}$,
答:△ODE的面积为2$\sqrt{10}$.
点评 本题考查了坐标与图形的性质,根据坐标的象限特点,能表示线段的长,并解决相应问题,如求图形面积等.

练习册系列答案
相关题目
4.20筐白菜,以每筐20千克为标准,超过或不足的千克数分别用正、负数来表示.记录如表:
(1)20筐白菜中,最重的一筐比最轻的一筐重5.5千克.
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价1.6元,则出售这20筐白菜可卖多少元?
| 与标准质量的差值 (单位:千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
| 筐数 | 1 | 4 | 2 | -1 | 4 | 8 |
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价1.6元,则出售这20筐白菜可卖多少元?
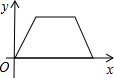 如图,是张老师晚上出门散步时离家的距离y与时间x之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )
如图,是张老师晚上出门散步时离家的距离y与时间x之间的函数图象,若用黑点表示张老师家的位置,则张老师散步行走的路线可能是( )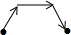


 已知:一次函数y=-x+8与两坐标轴分别交于A、B点,P为线段AB上的任意一点,过P点作PE⊥OA于点E,作PF⊥OB于F点,当长方形PEOF的面积最大时,P点坐标为(4,4).
已知:一次函数y=-x+8与两坐标轴分别交于A、B点,P为线段AB上的任意一点,过P点作PE⊥OA于点E,作PF⊥OB于F点,当长方形PEOF的面积最大时,P点坐标为(4,4).