题目内容
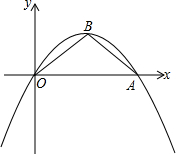 如图,当抛物线y=ax2+bx+c经过点A(4
如图,当抛物线y=ax2+bx+c经过点A(4| 3 |
| 3 |
(1)若△ABO内接于⊙P,求⊙P的半径;
(2)求该抛物线的解析式.
考点:圆的综合题
专题:
分析:(1)由抛物线的对称性可知△ABC是等腰三角形,所以内接于⊙P的圆心P在OA的垂直平分线上,即作AB的垂直平分线角OA于D,连接OP,设⊙P的半径为r,利用勾股定理建立关于r的方程,解方程即可求出r值;
(2)把点A(4
,0)和点B(2
,2)及原点O(0,0)代入抛物线的解析式y=ax2+bx+c求出a,b,c的值即可.
(2)把点A(4
| 3 |
| 3 |
解答:解:(1)作AB的垂直平分线角OA于D,连接OP,设⊙P的半径为r,
∵点A(4
,0),点B(2
,2),
∴OD=2
,BD=2,
∴DP=r-2,
在Rt△OPD中,DP2+OD2=OP2,
∴(r-2)2+(2
)2=r2,
∴r=4,
即⊙P的半径是4;
(2)把点A(4
,0)和点B(2
,2)及原点O(0,0)代入抛物线的解析式y=ax2+bx+c得:
,
解得:
,
∴抛物线的解析式是y=-
x2+
x.
∵点A(4
| 3 |
| 3 |
∴OD=2
| 3 |
∴DP=r-2,

在Rt△OPD中,DP2+OD2=OP2,
∴(r-2)2+(2
| 3 |
∴r=4,
即⊙P的半径是4;
(2)把点A(4
| 3 |
| 3 |
|
解得:
|
∴抛物线的解析式是y=-
| 1 |
| 6 |
2
| ||
| 3 |
点评:本题综合考查了圆的有关知识,用到的知识点由垂直平分线的性质、抛物线的性质、等腰三角形的判定和性质、勾股定理的运用以及利用待定系数法求二次函数的解析式,题目的综合性较强,难度中等.

练习册系列答案
相关题目
 在锐角△ABC中,∠ABC=45°,CD⊥AB,D是垂足,BD=4,M、N分别是BD、BC上动点,则CM+MN的最小值是
在锐角△ABC中,∠ABC=45°,CD⊥AB,D是垂足,BD=4,M、N分别是BD、BC上动点,则CM+MN的最小值是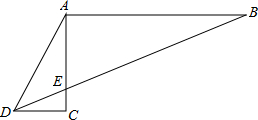 如图所示,已知∠C=90°,AB⊥AC,D、E、B在一直线上,∠ADE=2∠EDC,求证:BE=2AD.
如图所示,已知∠C=90°,AB⊥AC,D、E、B在一直线上,∠ADE=2∠EDC,求证:BE=2AD.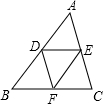 如图,在△ABC中,AB=4,BC=5,AC=6,D、E、F分别是AB、AC、BC边上的点,求DE+DF+EF的最小值.
如图,在△ABC中,AB=4,BC=5,AC=6,D、E、F分别是AB、AC、BC边上的点,求DE+DF+EF的最小值.