题目内容
一元二次方程x2-3x+1=0的两个根分别是x1,x2,则x
x2+x1x
的值是 .
2 1 |
2 2 |
考点:根与系数的关系
专题:
分析:先由根与系数的关系得出x1+x2=3,x1x2=1,再把所求代数式x
x2+x1x
变形为两根之积或两根之和的形式,代入数值计算即可.
2 1 |
2 2 |
解答:解:∵一元二次方程x2-3x+1=0的两个根分别是x1,x2,
∴x1+x2=3,x1x2=1,
∴x
x2+x1x
=x1x2(x1+x2)=1×3=3.
故答案为3.
∴x1+x2=3,x1x2=1,
∴x
2 1 |
2 2 |
故答案为3.
点评:本题考查了根与系数的关系:x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-
,x1x2=
.将根与系数的关系与代数式变形相结合解题是一种经常使用的解题方法.
| b |
| a |
| c |
| a |

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
以a、b、c为边,不能组成直角三角形的( )
| A、a=6,b=8,c=10 | ||||||
B、a=1,b=
| ||||||
| C、a=24,b=7,c=25 | ||||||
D、a=
|
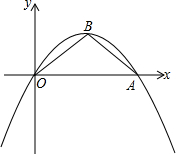 如图,当抛物线y=ax2+bx+c经过点A(4
如图,当抛物线y=ax2+bx+c经过点A(4