题目内容
 在锐角△ABC中,∠ABC=45°,CD⊥AB,D是垂足,BD=4,M、N分别是BD、BC上动点,则CM+MN的最小值是
在锐角△ABC中,∠ABC=45°,CD⊥AB,D是垂足,BD=4,M、N分别是BD、BC上动点,则CM+MN的最小值是考点:轴对称-最短路线问题
专题:
分析:作△ABC关于直线AB的对称△ABC′,C′是C的对称点,连接C′N交AB于M′,由于∠ABC=45°,所以∠CBC′=90°,所以点N在点B时,CM+MN有最小值,
再根据BC=4
,即可求出BC′的长.
再根据BC=4
| 2 |
解答: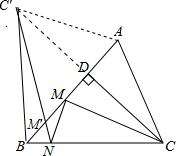 解:作△ABC关于直线AB的对称△ABC′,C′是C的对称点,连接C′N交AB于M′,
解:作△ABC关于直线AB的对称△ABC′,C′是C的对称点,连接C′N交AB于M′,
∵∠ABC=45°,
∴∠ABC′=45°,
∴∠CBC′=90°,
∴点N在点B时,CM+MN有最小值,
则BC′即为CM+MN的最小值,
∵C′是C的对称点,CD⊥AB,
∴C、D、C′三点共线,
∴△CBC′是等腰直角三角形,
∴BC′=BC,
∵∠ABC=45°,CD⊥AB,BD=4,
∴△BDC是等腰直角三角形,
∴BC=
BD=4
,
∴BC′=4
,
故答案为4
.
 解:作△ABC关于直线AB的对称△ABC′,C′是C的对称点,连接C′N交AB于M′,
解:作△ABC关于直线AB的对称△ABC′,C′是C的对称点,连接C′N交AB于M′,∵∠ABC=45°,
∴∠ABC′=45°,
∴∠CBC′=90°,
∴点N在点B时,CM+MN有最小值,
则BC′即为CM+MN的最小值,
∵C′是C的对称点,CD⊥AB,
∴C、D、C′三点共线,
∴△CBC′是等腰直角三角形,
∴BC′=BC,
∵∠ABC=45°,CD⊥AB,BD=4,
∴△BDC是等腰直角三角形,
∴BC=
| 2 |
| 2 |
∴BC′=4
| 2 |
故答案为4
| 2 |
点评:本题考查的是轴对称-最短路线问题,根据题意作出辅助线,构造出等腰直角三角形,利用等腰直角三角形求解是解答此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
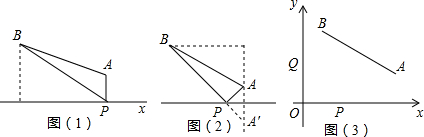
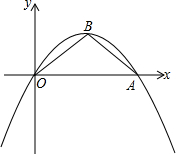 如图,当抛物线y=ax2+bx+c经过点A(4
如图,当抛物线y=ax2+bx+c经过点A(4 如图,大正方形的边长为a+b,小正方形的边长为2,则阴影部分的面积为
如图,大正方形的边长为a+b,小正方形的边长为2,则阴影部分的面积为