题目内容
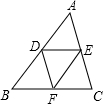 如图,在△ABC中,AB=4,BC=5,AC=6,D、E、F分别是AB、AC、BC边上的点,求DE+DF+EF的最小值.
如图,在△ABC中,AB=4,BC=5,AC=6,D、E、F分别是AB、AC、BC边上的点,求DE+DF+EF的最小值.考点:轴对称-最短路线问题
专题:
分析:根据轴对称的性质和两点之间线段最短的性质来计算.
解答: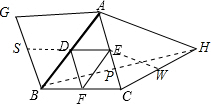 解:如图,作出△ABC关于AB对称的△ABG,△ABC关于AC对称的△ACH,
解:如图,作出△ABC关于AB对称的△ABG,△ABC关于AC对称的△ACH,
则点F关于AB的对称点为S,关于AC的对称点为W,
当S,D,E,W在同一直线上,且点S与点F重合在点B,
点W在点H时,DE+DF+EF有最小值,
∵AC⊥BH,且平分BH,
∴BP2=AB2-AP2=BC2-CP2,
设AP=x,则CP=6-x,
∴42-x2=52-(6-x)2,解得,x=
,
∴BP=
=
故DE+DF+EF的最小值=2×BP=2×
=
.
 解:如图,作出△ABC关于AB对称的△ABG,△ABC关于AC对称的△ACH,
解:如图,作出△ABC关于AB对称的△ABG,△ABC关于AC对称的△ACH,则点F关于AB的对称点为S,关于AC的对称点为W,
当S,D,E,W在同一直线上,且点S与点F重合在点B,
点W在点H时,DE+DF+EF有最小值,
∵AC⊥BH,且平分BH,
∴BP2=AB2-AP2=BC2-CP2,
设AP=x,则CP=6-x,
∴42-x2=52-(6-x)2,解得,x=
| 9 |
| 4 |
∴BP=
| AB2-AP2 |
5
| ||
| 4 |
故DE+DF+EF的最小值=2×BP=2×
5
| ||
| 4 |
5
| ||
| 2 |
点评:本题考查了利用轴对称图形的性质和两点之间线段最短的性质求解.

练习册系列答案
相关题目
 如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠DAC等于( )
如图,OA=OB,OC=OD,∠O=50°,∠D=35°,则∠DAC等于( )| A、60° | B、50° |
| C、85° | D、30° |
函数y=
x2+1与y=
x2+2的图象的不同之处是( )
| 1 |
| 2 |
| 1 |
| 2 |
| A、对称轴 | B、开口方向 |
| C、顶点 | D、形状 |
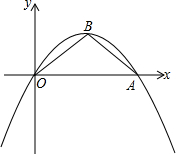 如图,当抛物线y=ax2+bx+c经过点A(4
如图,当抛物线y=ax2+bx+c经过点A(4