题目内容
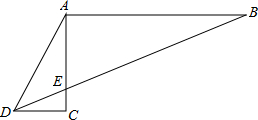 如图所示,已知∠C=90°,AB⊥AC,D、E、B在一直线上,∠ADE=2∠EDC,求证:BE=2AD.
如图所示,已知∠C=90°,AB⊥AC,D、E、B在一直线上,∠ADE=2∠EDC,求证:BE=2AD.考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:证明题
分析:取BE的中点F,连接AF,根据直角三角形斜边上的中线等于斜边的一半可得AF=BF=
BE,根据等边对等角可得∠B=∠BAF,在求出AB∥CD,根据两直线平行,内错角相等可得∠B=∠EDC,再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AFD=2∠B,从而得到∠AFD=∠ADE,根据等角对等边可得AD=AF,然后等量代换即可得证.
| 1 |
| 2 |
解答: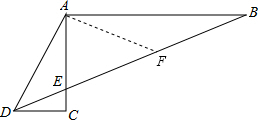 证明:如图,取BE的中点F,连接AF,
证明:如图,取BE的中点F,连接AF,
∵AB⊥AC,
∴AF=BF=
BE,
∴∠B=∠BAF,
∵∠C=90°,AB⊥AC,
∴AB∥CD,
∴∠B=∠EDC,
由三角形的外角性质得,∠AFD=∠B+∠BAF=2∠B,
∵∠ADE=2∠EDC,
∴∠AFD=∠ADE,
∴AD=AF,
∴AD=
BE,
∴BE=2AD.
 证明:如图,取BE的中点F,连接AF,
证明:如图,取BE的中点F,连接AF,∵AB⊥AC,
∴AF=BF=
| 1 |
| 2 |
∴∠B=∠BAF,
∵∠C=90°,AB⊥AC,
∴AB∥CD,
∴∠B=∠EDC,
由三角形的外角性质得,∠AFD=∠B+∠BAF=2∠B,
∵∠ADE=2∠EDC,
∴∠AFD=∠ADE,
∴AD=AF,
∴AD=
| 1 |
| 2 |
∴BE=2AD.
点评:本题考查了直角三角形斜边上的中线等于斜边的一半的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,等边对等角和等角对等边,熟记各性质并作辅助线构造出等腰三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
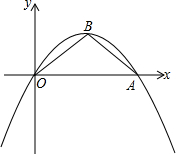 如图,当抛物线y=ax2+bx+c经过点A(4
如图,当抛物线y=ax2+bx+c经过点A(4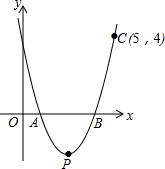 如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4).
如图,抛物线y=ax2-5x+4a与x轴交于点A,B,且过点C(5,4). 如图,大正方形的边长为a+b,小正方形的边长为2,则阴影部分的面积为
如图,大正方形的边长为a+b,小正方形的边长为2,则阴影部分的面积为