题目内容
14.解方程:2x+$\frac{x-1}{2}$=3-$\frac{2x-1}{3}$.分析 方程去分母,去括号,移项合并,把x系数化为1,即可求出解.
解答 解:去分母得:12x+3(x-1)=18-2(2x-1),
去括号得:12x+3x-3=18-4x+2,
移项合并得:19x=23,
解得:x=$\frac{23}{19}$.
点评 此题考查了解一元一次方程,熟练掌握运算法则是解本题的关键.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
4.下列各式不是单项式的是( )
| A. | 4x | B. | 2x2y | C. | -5 | D. | n-2 |
2.用四舍五入法将0.0257精确到0.001结果是( )
| A. | 0.03 | B. | 0.026 | C. | 0.025 | D. | 0.0257 |
19.下列说法错误的是( )
| A. | 两点确定一条直线 | |
| B. | 在同一平面内,过一点有且只有一条直线与已知直线垂直 | |
| C. | 过一点有且只有一条直线与已知直线平行 | |
| D. | 若两条直线相交所成的角是直角,则这两条直线互相垂直 |
6.1号探测气球从海拔5米处出发,以1米/分的速度上升.与此同时,2号探测气球从海拔15米处出发,以0.5米/分的速度上升,两个气球都匀速上升了50分钟.
设气球球上升时间为x分(0≤x≤50)
(1)根据题意,填写下表:
(2)在某时刻两个气球能否位于同一高度?如果能,这时气球上升了多长时间?位于什么高度?如果不能,请说明理由;
(3)当两个气球所在位置的海拔相差7.5米时,这时气球上升了多长时间?
设气球球上升时间为x分(0≤x≤50)
(1)根据题意,填写下表:
| 上升时间/分 | 10 | 30 | … | x |
| 1号探测气球所在位置的海拔/米 | 15 | 35 | … | x+5 |
| 2号探测气球所在位置的海拔/米 | 20 | 30 | … | 0.5x+15 |
(3)当两个气球所在位置的海拔相差7.5米时,这时气球上升了多长时间?
4.计算(a2bc)3的结果是( )
| A. | a3b3c | B. | a9b3c3 | C. | a3bc3 | D. | a6b3c3 |
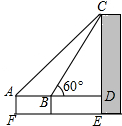 如图,为了测量某建筑物CE的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是45°,然后在水平地面上向建筑物前进了20m,此时自B处测得建筑物顶部的仰角是60°,已知测角仪的高度是1m,请你计算出该建筑物的高度(取$\sqrt{3}$≈1.732,结果精确到1m).
如图,为了测量某建筑物CE的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是45°,然后在水平地面上向建筑物前进了20m,此时自B处测得建筑物顶部的仰角是60°,已知测角仪的高度是1m,请你计算出该建筑物的高度(取$\sqrt{3}$≈1.732,结果精确到1m). 如图,AB∥CD,∠BAE=135°,∠DCE=40°,则∠AEC=85度.
如图,AB∥CD,∠BAE=135°,∠DCE=40°,则∠AEC=85度.