题目内容
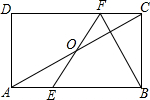 如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,EF与对角线AC交于O点.
如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,EF与对角线AC交于O点.(1)求证:OE=OF;
(2)连接BF,若BE=BF,∠BEF=2∠BAC,BC=2
| 5 |
考点:矩形的性质,全等三角形的判定与性质,勾股定理
专题:
分析:(1)利用矩形的性质得出∠CAE=∠ACF,∠CFO=∠AEO,进而求出△AOE≌△COF(AAS),得出答案即可;
(2)首先求出∠BAC=30°,进而得出∠BEF=2∠OBE,利用AB=
求出即可.
(2)首先求出∠BAC=30°,进而得出∠BEF=2∠OBE,利用AB=
| AC2-BC2 |
解答: (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,
∴AB∥CD,
∴∠CAE=∠ACF,∠CFO=∠AEO,
在△AOE和△COF中
,
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:连接OB,
∵BF=BE,OE=OF,
∴BO⊥EF,
由(1)知,△AOE≌△COF,
∴OA=OC,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BO=
AC=OA,
∴∠BAC=∠OBA,
又∠BEF=2∠BAC,
∴∠BEF=2∠OBE,
而Rt△OBE中,∠BEO+∠OBE=90°,
∴∠BAC=30°,
∴AC=2BC=2×2
=4
,
∴AB=
=
=
=2
.
 (1)证明:∵四边形ABCD是矩形,
(1)证明:∵四边形ABCD是矩形,∴AB∥CD,
∴∠CAE=∠ACF,∠CFO=∠AEO,
在△AOE和△COF中
|
∴△AOE≌△COF(AAS),
∴OE=OF;
(2)解:连接OB,
∵BF=BE,OE=OF,
∴BO⊥EF,
由(1)知,△AOE≌△COF,
∴OA=OC,
∵四边形ABCD是矩形,
∴∠ABC=90°,
∴BO=
| 1 |
| 2 |
∴∠BAC=∠OBA,
又∠BEF=2∠BAC,
∴∠BEF=2∠OBE,
而Rt△OBE中,∠BEO+∠OBE=90°,
∴∠BAC=30°,
∴AC=2BC=2×2
| 5 |
| 5 |
∴AB=
| AC2-BC2 |
| 80-20 |
| 60 |
| 15 |
点评:此题主要考查了矩形的性质以及勾股定理和全等三角形的判定与性质等知识,得出△AOE≌△COF(AAS)是解题关键.

练习册系列答案
 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目
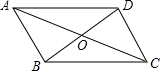 如图,在?ABCD中,已知对角线AC、BD相交于点O.
如图,在?ABCD中,已知对角线AC、BD相交于点O. 如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整,并在横线上填写理由:
如图,EF∥AD,∠1=∠2,∠BAC=70°,将求∠AGD的过程填写完整,并在横线上填写理由: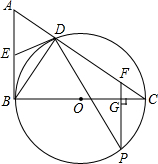 如图,在Rt△ABC中,∠ABC=90°,以BC为直径的⊙O与AC相交于点D,点E为AB的中点,点P是⊙O上一点,过点P作PF⊥BC交BC于点G,交AC于点F.
如图,在Rt△ABC中,∠ABC=90°,以BC为直径的⊙O与AC相交于点D,点E为AB的中点,点P是⊙O上一点,过点P作PF⊥BC交BC于点G,交AC于点F. 如图是一张铁片的示意图
如图是一张铁片的示意图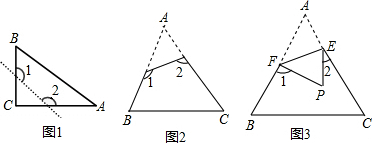
 如图,剪刀在使用的过程中,随着两个把手之间的夹角(∠DOC)逐渐变大,剪刀刀刃之间的夹角(∠AOB)也相应
如图,剪刀在使用的过程中,随着两个把手之间的夹角(∠DOC)逐渐变大,剪刀刀刃之间的夹角(∠AOB)也相应