题目内容
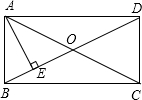 如图,矩形ABCD的对角线AC,BD交于点F,∠AFB=45°AE⊥BD,垂足是点E,则∠BAE的大小为( )
如图,矩形ABCD的对角线AC,BD交于点F,∠AFB=45°AE⊥BD,垂足是点E,则∠BAE的大小为( )| A、15° | B、22.5° |
| C、30° | D、45° |
考点:矩形的性质
专题:
分析:易证∠BAE=∠ADE,根据矩形对角线相等且互相平分的性质,可得∠OAB=∠OBA,在Rt△ABD中,已知∠OBA即可求得∠BAE的大小.
解答:解:∵四边形ABCD是矩形,AE⊥BD,
∴∠BAE+∠ABD=90°,∠ADE+∠ABD=90°,
∴∠BAE=∠ADE
∵矩形对角线相等且互相平分,
∴∠OAB=∠OBA=
=67.5°,
∴∠BAE=∠ADE=90-67.5°=22.5°,
故选 B.
∴∠BAE+∠ABD=90°,∠ADE+∠ABD=90°,
∴∠BAE=∠ADE
∵矩形对角线相等且互相平分,
∴∠OAB=∠OBA=
| 180°-45° |
| 2 |
∴∠BAE=∠ADE=90-67.5°=22.5°,
故选 B.
点评:本题考查了矩形对角线相等且互相平分的性质,考查了等腰三角形底角相等的性质,本题中计算∠OAB的值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在下列命题中,真命题是( )
| A、有两边平行的四边形是平行四边形 |
| B、对角线互相垂直平分的四边形是菱形 |
| C、有一个角是直角的四边形是矩形 |
| D、有一个角是直角且有一组邻边相等的四边形是正方形 |
已知a2+b2+4a-b+4
=0,则a-b的值是( )
| 1 |
| 4 |
A、1
| ||
B、2
| ||
C、-2
| ||
D、-1
|
72010-72008不能被以下哪个整数整除?( )
| A、9 | B、8 | C、7 | D、6 |
 已知:如图,点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
已知:如图,点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=- 如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )