题目内容
 如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )
如图,E是边长为1的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC于点Q,PR⊥BE于点R,则PQ+PR的值是( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:正方形的性质
专题:
分析:连接BP,利用面积法求解,PQ+PR的值等于C点到BE的距离,即正方形对角线的一半.
解答:解:连接BP,过C作CM⊥BD,
∵S△BCE=S△BPE+S△BPC
=BC×PQ×
+BE×PR×
=BC×(PQ+PR)×
=BE×CM×
,
BC=BE,
∴PQ+PR=CM,
∵BE=BC=1且正方形对角线BD=
=
,
又∵BC=CD,CM⊥BD,
∴M为BD中点,又△BDC为直角三角形,
∴CM=
BD=
,
即PQ+PR值是
.
故选D.
∵S△BCE=S△BPE+S△BPC
=BC×PQ×
| 1 |
| 2 |
| 1 |
| 2 |
=BC×(PQ+PR)×
| 1 |
| 2 |
=BE×CM×
| 1 |
| 2 |
BC=BE,

∴PQ+PR=CM,
∵BE=BC=1且正方形对角线BD=
| 2BC |
| 2 |
又∵BC=CD,CM⊥BD,
∴M为BD中点,又△BDC为直角三角形,
∴CM=
| 1 |
| 2 |
| ||
| 2 |
即PQ+PR值是
| ||
| 2 |
故选D.
点评:本题考查了正方形的性质以及勾股定理的运用,解题关键是作出正确的辅助线,利用全等三角形的判定和性质的应用,来化简题目.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
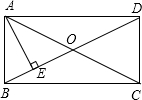 如图,矩形ABCD的对角线AC,BD交于点F,∠AFB=45°AE⊥BD,垂足是点E,则∠BAE的大小为( )
如图,矩形ABCD的对角线AC,BD交于点F,∠AFB=45°AE⊥BD,垂足是点E,则∠BAE的大小为( )| A、15° | B、22.5° |
| C、30° | D、45° |
某人设计了一个游戏,在网吧征求了三位游戏迷的意见,就宣传“本游戏深受大家欢迎”,这种做法是错误的,原因是( )
| A、没有经过专家鉴定 |
| B、应调查4位游戏迷 |
| C、调查数量太少,且不具有代表性 |
| D、以上都不对 |
 如图:在△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=4cm,则AD=( )cm.
如图:在△ABC中,∠ACB=90°,CD是高,∠A=30°,BD=4cm,则AD=( )cm.| A、14 | B、6 | C、9 | D、12 |
将多项式x2+9加上一个整式,使它成为完全平方式,不能满足上述条件的整式是( )
| A、-9 | B、-6x | C、6x | D、9 |
在平面直角坐标系中,将点A(2,1)先向下平移2个单位长度,再向左平移1个单位长度,得到点A1,则点A1的坐标为( )
| A、(2,-1) |
| B、(-2,1) |
| C、(1,-1) |
| D、(1,2) |
 有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是
有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是