题目内容
 已知:如图,点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-
已知:如图,点P的坐标为(m,0),在x轴上存在点Q(不与P点重合),以PQ为边作正方形PQMN,使点M落在反比例函数y=-| 2 |
| x |
考点:正方形的性质,反比例函数图象上点的坐标特征
专题:分类讨论
分析:设正方形的边长为a,然后分①点Q在点P的左边,表示出点M的坐标,再代入反比例函数解析式求解即可;②点Q在点P的右边时,表示出点M的坐标,再代入反比例函数解析式求解.
解答: 解:设正方形的边长为a,
解:设正方形的边长为a,
①点Q在点P的左边时,若点M在第二象限,则a>6,M(6-a,a),
∵点M在反比例函数图象上,
∴-
=a,
整理得,a2-6a-2=0,
解得a1=3+
,a2=3-
(舍去),
此时点M的坐标为(3-
,3+
),
若点M在第四象限,则a<6,点M(6-a,-a),
∵点M在反比例函数图象上,
∴-
=-a,
整理得,a2-6a+2=0,
解得a1=3+
,a2=3-
,
此时,点M的坐标为(3-
,-3-
)或(3+
,-3+
);
②点Q在点P的右边时,点M的坐标为(6+a,-a),
∵点M在反比例函数图象上,
∴-
=-a,
整理得,a2+6a-2=0,
解得a1=-3+
,a2=-3-
(舍去),
此时,点M(3+
,3-
),
综上所述,点M的坐标为(3-
,3+
)或(3+
,3-
)或(3-
,-3-
)或(3+
,-3+
).
故答案为:(3-
,3+
)或(3+
,3-
)或(3-
,-3-
)或(3+
,-3+
).
 解:设正方形的边长为a,
解:设正方形的边长为a,①点Q在点P的左边时,若点M在第二象限,则a>6,M(6-a,a),
∵点M在反比例函数图象上,
∴-
| 2 |
| 6-a |
整理得,a2-6a-2=0,
解得a1=3+
| 11 |
| 11 |
此时点M的坐标为(3-
| 11 |
| 11 |
若点M在第四象限,则a<6,点M(6-a,-a),
∵点M在反比例函数图象上,
∴-
| 2 |
| 6-a |
整理得,a2-6a+2=0,
解得a1=3+
| 7 |
| 7 |
此时,点M的坐标为(3-
| 7 |
| 7 |
| 7 |
| 7 |
②点Q在点P的右边时,点M的坐标为(6+a,-a),
∵点M在反比例函数图象上,
∴-
| 2 |
| 6+a |
整理得,a2+6a-2=0,
解得a1=-3+
| 11 |
| 11 |
此时,点M(3+
| 11 |
| 11 |
综上所述,点M的坐标为(3-
| 11 |
| 11 |
| 11 |
| 11 |
| 7 |
| 7 |
| 7 |
| 7 |
故答案为:(3-
| 11 |
| 11 |
| 11 |
| 11 |
| 7 |
| 7 |
| 7 |
| 7 |
点评:本题考查了正方形的性质,反比例函数图象上点的坐标特征,设出正方形的边长然后表示出点M的坐标是解题的关键,难点在于分情况讨论.

练习册系列答案
相关题目
一个不透明的袋中装有20个白球和若干个黄球,它们除颜色不同外,其余都完全相同,若从袋中随机地摸出一个球是白球的概率为
,则袋中黄球的个数为( )
| 1 |
| 3 |
| A、60个 | B、50个 |
| C、40个 | D、30个 |
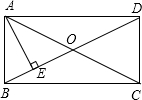 如图,矩形ABCD的对角线AC,BD交于点F,∠AFB=45°AE⊥BD,垂足是点E,则∠BAE的大小为( )
如图,矩形ABCD的对角线AC,BD交于点F,∠AFB=45°AE⊥BD,垂足是点E,则∠BAE的大小为( )| A、15° | B、22.5° |
| C、30° | D、45° |
某人设计了一个游戏,在网吧征求了三位游戏迷的意见,就宣传“本游戏深受大家欢迎”,这种做法是错误的,原因是( )
| A、没有经过专家鉴定 |
| B、应调查4位游戏迷 |
| C、调查数量太少,且不具有代表性 |
| D、以上都不对 |
 有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是
有一数值转换器,原理如图所示,若开始输入x的值是7,可发现第1次输出的结果是12,第2次输出的结果是6,第3次输出的结果是