题目内容
13.先化简再求值:$\frac{x-1}{x-2}$÷(1-$\frac{2x-5}{{x}^{2}-4}$),并选一个你喜欢的数代入求值.分析 先算括号内的减法,把除法变成乘法,根据分式的乘法法则进行化简,最后取一个符合的数代入求出即可.
解答 解:$\frac{x-1}{x-2}$÷(1-$\frac{2x-5}{{x}^{2}-4}$)
=$\frac{x-1}{x-2}$÷[$\frac{(x+2)(x-2)}{(x+2)(x-2)}$-$\frac{2x-5}{(x+2)(x-2)}$]
=$\frac{x-1}{x-2}$÷$\frac{{x}^{2}-2x+1}{(x+2)(x-2)}$
=$\frac{x-1}{x-2}$•$\frac{(x+2)(x-2)}{(x-1)^{2}}$
=$\frac{x+2}{x-1}$,
∵根据已知算式得出x-1≠0,x+2≠0,x-2≠0,
∴x不可取1,2,-2,
∴取x=0,代入得:原式=$\frac{0+2}{0-1}$=-2.
点评 本题考查了分式的混合运算和求值的应用,能综合运用分式的运算法则进行化简是解此题的关键,综合比较强,有一定的难度,注意运算顺序.

练习册系列答案
相关题目
8.$\sqrt{35}$×$\sqrt{\frac{1}{7}}$的计算结果估计在( )
| A. | 1.0至1.5之间 | B. | 1.5至2.0之间 | C. | 2.0至2.5之间 | D. | 2.5至3之间 |
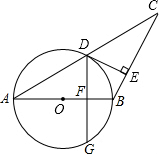 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为E.