题目内容
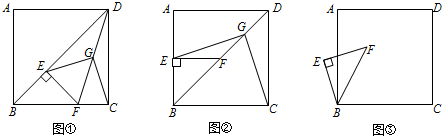
 如图,在?ABCD中,点E为BC上一点,F为DE上一点,DA=DE,EB=EF,求证:
如图,在?ABCD中,点E为BC上一点,F为DE上一点,DA=DE,EB=EF,求证:(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)利用平行四边形的对边相互平行和平行线的性质得到∠DAE=∠AEB,然后结合等腰△ADE的性质推知∠DAE=∠AEF,则∠AEB=∠AEF.然后结合这两个三角形中的相关线段对应相等,可以证得结论;
(2)利用(1)中全等三角形的性质和平行四边形对角相等的性质,结合三角形外角定理证得结论.
(2)利用(1)中全等三角形的性质和平行四边形对角相等的性质,结合三角形外角定理证得结论.
解答: 证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB.
又∵DA=DE,
∴∠DAE=∠AEF,则∠AEB=∠AEF.
在△ABE与△AFE中,
,
∴△ABE≌△AFE(SAS);
(2)由(1)知△ABE≌△AFE,则∠ABE=∠AFE.
∵四边形ABCD是平行四边形,
∴∠ADC=∠B.
由∵∠AFE=∠DAF+∠ADF,∠ADC=∠CDE+∠ADF,
∴∠FAD+∠ADF=∠CDE+∠ADF,
∴∠FAD=∠CDE.
 证明:(1)∵四边形ABCD是平行四边形,
证明:(1)∵四边形ABCD是平行四边形,∴AD∥BC,
∴∠DAE=∠AEB.
又∵DA=DE,
∴∠DAE=∠AEF,则∠AEB=∠AEF.
在△ABE与△AFE中,
|
∴△ABE≌△AFE(SAS);
(2)由(1)知△ABE≌△AFE,则∠ABE=∠AFE.
∵四边形ABCD是平行四边形,
∴∠ADC=∠B.
由∵∠AFE=∠DAF+∠ADF,∠ADC=∠CDE+∠ADF,
∴∠FAD+∠ADF=∠CDE+∠ADF,
∴∠FAD=∠CDE.
点评:本题考查了平行四边形的性质、全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
 已知B是线段AC延长线一点.D是AB中点,E是BC中点,DE=6,求AC的长度.
已知B是线段AC延长线一点.D是AB中点,E是BC中点,DE=6,求AC的长度. 如图,在△ABC中,BC=2+2
如图,在△ABC中,BC=2+2