题目内容
如图，在△ABC中，BC=2+2| 3 |
考点：直线与圆的位置关系
专题：
分析：首先过点A作AD⊥BC于点D，进而表示出BD的长，即可得出AD的长，再利用直线与圆的位置关系求出即可．
解答：
解：过点A作AD⊥BC于点D，
设AD=x，
∵∠B=30°，∠C=45°，
∴DC=x，BD=
x，
∴x+
x=2+2
，
解得：x=2，
即AD=2，
当①相切，⊙A的半径r=2，
当②相交，⊙A的半径r＞2，
当③相离，⊙A的半径r＜2．
解：过点A作AD⊥BC于点D，设AD=x，
∵∠B=30°，∠C=45°，
∴DC=x，BD=
| 3 |
∴x+
| 3 |
| 3 |
解得：x=2，
即AD=2，
当①相切，⊙A的半径r=2，
当②相交，⊙A的半径r＞2，
当③相离，⊙A的半径r＜2．
点评：此题主要考查了直线与圆的位置关系，正确把握直线与圆的位置关系判定方法是解题关键．
练习册系列答案
相关题目
如图，在?ABCD中，点E为BC上一点，F为DE上一点，DA=DE，EB=EF，求证：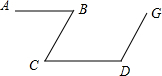
如图，∠ABC=∠BCD，∠ABC+∠CDG=180°，试问：BC与GD平行吗？若平行，请说明理由．
利用图中所给的基本图案，通过平移、旋转和轴对称三种变换设计图案，所设计的图案要包括4个基本图案．