题目内容
12.如图,线段AB=1,点P1是线段AB的黄金分割点(AP1<BP1)(即P1B2=AP1•AB),点P2是线段AP1的黄金分割点(AP2<P1P2),点P3是线段AP2的黄金分割点(AP3<P2P3),…,依此类推,则线段AP2015的长度是($\frac{3-\sqrt{5}}{2}$)2015.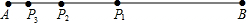
分析 根据把一条线段分成两部分,使其中较长的线段为全线段与较短线段的比例中项,这样的线段分割叫做黄金分割,它们的比值($\frac{\sqrt{5}-1}{2}$)叫做黄金比进行解答即可.
解答 解:根据黄金比的比值,BP1=$\frac{\sqrt{5}-1}{2}$,
则AP1=1-$\frac{\sqrt{5}-1}{2}$=$\frac{3-\sqrt{5}}{2}$,
AP2=($\frac{3-\sqrt{5}}{2}$)2,
AP3=($\frac{3-\sqrt{5}}{2}$)3,
…
依此类推,则线段AP2015的长度是($\frac{3-\sqrt{5}}{2}$)2015
故答案为:($\frac{3-\sqrt{5}}{2}$)2015.
点评 本题考查的是黄金分割的知识,理解黄金分割的概念,找出黄金分割中成比例的对应线段是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知四边形ABCD的四条边分别是a、b、c、d.其中a、c是对边,且a2+b2+c2+d2=2ac+2bd,则四边形一定是( )
| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
4.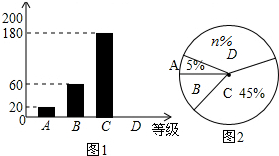 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
(1)本次参与调查的学生共有400人,m=15%,n=35.
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
 据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:
据报道:“国际剪刀石头布协会”提议将“剪刀石头布”作为奥运会比赛项目.为了调查学生对这个提议的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解;B、比较了解;C、基本了解;D、不了解.根据调查统计结果,绘制了不完整的三种统计图表,请结合统计图表,回答下列问题:| 对提议的了解程度 | 百分比 |
| A、非常了解 | 5% |
| B、比较了解 | m |
| C、基本了解 | 45% |
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是126度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于“剪刀石头布”知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个求上的数字和为奇数,则小明去;否则小刚去,请用树状图或列表法说明这个游戏规则是否公平.
1.直线y=3x+m的图象一定经过( )
| A. | 第一、二象限 | B. | 第二、四象限 | C. | 第一、三象限 | D. | 第二、三象限 |
2.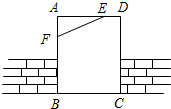 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )| A. | 两点之间,线段最短 | B. | 直角三角形的两个锐角互余 | ||
| C. | 三角形三个内角和等于180° | D. | 三角形具有稳定性 |
 ”可以得到美丽的“中国结”图案,左边四个图案是由“
”可以得到美丽的“中国结”图案,左边四个图案是由“
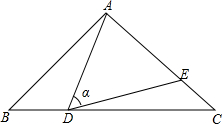 如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论:
如图,在△ABC中,AB=AC=10,点D是边BC上一动点(不与B、C重合),∠ADE=∠B=α,DE交AC于点E,且cosα=$\frac{4}{5}$.下列结论: