题目内容
12. 如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=$\sqrt{6}$,则AE=2(提示:可过点A作BD的垂线)
如图,在四边形ABCD中,对角线AC、BD相交于点E,∠DAB=∠CDB=90°,∠ABD=45°,∠DCA=30°,AB=$\sqrt{6}$,则AE=2(提示:可过点A作BD的垂线)
分析 过A作AF⊥BD,交BD于点F,由三角形ABD为等腰直角三角形,利用三线合一得到AF为中线,利用直角三角形斜边上的中线等于斜边的一半求出AF的长,在直角三角形AEF中,利用30度角所对的直角边等于斜边的一半求出AE的长即可.
解答 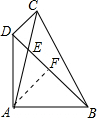 解:过A作AF⊥BD,交BD于点F,
解:过A作AF⊥BD,交BD于点F,
∵AD=AB,∠DAB=90°,
∴AF为BD边上的中线,
∴AF=$\frac{1}{2}$BD,
∵AB=AD=$\sqrt{6}$,
∴根据勾股定理得:BD=$\sqrt{6+6}$=2$\sqrt{3}$,
∴AF=$\sqrt{3}$,
在Rt△AFE中,∠EAF=∠DCA=30°,
∴EF=$\frac{1}{2}$AE,
设EF=x,则有AE=2x,
根据勾股定理得:x2+3=4x2,
解得:x=1,
则AE=2.
故答案为:2
点评 此题考查了勾股定理,含30度直角三角形的性质,以及等腰三角形的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目
7. 如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )
如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )
 如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )
如图,边长为1的小正方形构成的网格中,⊙O半径为1,圆心O在格点上,则tan∠AED=( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
17. 如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )
如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )
 如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )
如图,点P是△ABC内一点,且PD=PE=PF,则点P是( )| A. | △ABC三边垂直平分线的交点 | B. | △ABC三条角平分线的交点 | ||
| C. | △ABC三条高所在直线的交点 | D. | △ABC三条中线的交点 |
4.某商店举办促销活动,促销的方法是将原价x元的衣服以$\frac{3}{5}$(x-10)元出售,则下列说法中,能正确表达该商店促销方法的是( )
| A. | 原价减去10元后再打6折 | B. | 原价打6折后再减去10元 | ||
| C. | 原价减去10元后再打4折 | D. | 原价打4折后再减去10元 |
 如图所示的是一段楼梯,高BC=3m,斜边AB=5m,现计划在楼上铺地毯,至少需要地毯的长为7m.
如图所示的是一段楼梯,高BC=3m,斜边AB=5m,现计划在楼上铺地毯,至少需要地毯的长为7m.