题目内容
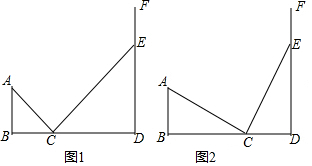
12. 如图,四边形ABCD,CDMF,MFEG都是正方形,BD,AE相交于点H,求tan∠AHB.
如图,四边形ABCD,CDMF,MFEG都是正方形,BD,AE相交于点H,求tan∠AHB.
分析 设正方形的边长为1,由勾股定理求得BD=$\sqrt{2}$,证△ADH∽△EBH得$\frac{DH}{BH}$=$\frac{AD}{BE}$=$\frac{1}{3}$,即可知BH=$\frac{3}{4}$BD=$\frac{3\sqrt{2}}{4}$,作AN⊥BD,有AN=BN=ABcos45°=$\frac{\sqrt{2}}{2}$、NH=BH-BN=$\frac{3\sqrt{2}}{4}$-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{4}$,最后由正切函数定义可得.
解答 解:设正方形的边长为1,
则BD=$\sqrt{A{D}^{2}+B{D}^{2}}$=$\sqrt{2}$,
∵AD∥BE,
∴△ADH∽△EBH,
∴$\frac{DH}{BH}$=$\frac{AD}{BE}$=$\frac{1}{3}$,
∴BH=$\frac{3}{4}$BD=$\frac{3\sqrt{2}}{4}$,
过点A作AN⊥BD于点N,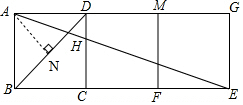
则AN=BN=ABcos45°=$\frac{\sqrt{2}}{2}$,
∴NH=BH-BN=$\frac{3\sqrt{2}}{4}$-$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{4}$,
∴tan∠AHB=$\frac{AN}{NH}$=$\frac{\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{4}}$=2.
点评 本题主要考查解直角三角形和相似三角形的判定与性质,解题的关键是利用相似三角形的判定与性质及三角函数的定义得出求正切值所需线段的长.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
13.在△ABC中,∠ACB=90°,BC=1,AC=2,则下列正确的是( )
| A. | sinA=$\frac{2\sqrt{5}}{5}$ | B. | tanA=$\frac{\sqrt{5}}{5}$ | C. | cosB=$\frac{\sqrt{5}}{5}$ | D. | tanB=$\frac{1}{2}$ |
3.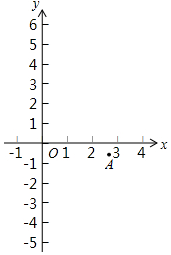 有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
下面是小东的探究过程,请补充完成:
(1)函数y=(x-1)(x-2)(x-3)的自变量x的取值范围是全体实数;
(2)下表是y与x的几组对应值.
①m=-60;
②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,-yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
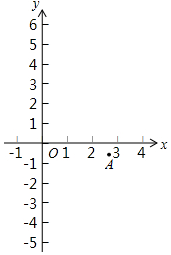 有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.
有这样一个问题:探究函数y=(x-1)(x-2)(x-3)的图象与性质.小东对函数y=(x-1)(x-2)(x-3)的图象与性质进行了探究.下面是小东的探究过程,请补充完成:
(1)函数y=(x-1)(x-2)(x-3)的自变量x的取值范围是全体实数;
(2)下表是y与x的几组对应值.
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| y | … | m | -24 | -6 | 0 | 0 | 0 | 6 | 24 | 60 | … |
②若M(-7,-720),N(n,720)为该函数图象上的两点,则n=11;
(3)在平面直角坐标系xOy中,A(xA,yA),B(xB,-yA)为该函数图象上的两点,且A为2≤x≤3范围内的最低点,A点的位置如图所示.
①标出点B的位置;
②画出函数y=(x-1)(x-2)(x-3)(0≤x≤4)的图象.
7.已知x与y之间的关系如表所示:
下面用x表示y的式子中,正确的是( )
| x | 1 | 2 | 3 | 4 | … |
| y | 0.6+3 | 0.6+6 | 0.6+9 | 0.6+12 | … |
| A. | y=0.6+x | B. | y=0.6+3x | C. | y=0.6×3+x | D. | y=0.6×3-x |
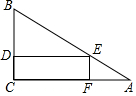 一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上.
一块三角形材料如图所示,∠A=30°,∠C=90°,AB=12,用这块材料剪出一个矩形CDEF,其中D、E、F分别在BC、AB、AC上.