题目内容
9.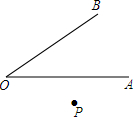 已知:如图,在∠AOB外有一点P,
已知:如图,在∠AOB外有一点P,(1)试画出点P关于直线OA的对称点P1,再画出点P1关于直线OB的对称点P2;
(2)试探索∠POP2与∠AOB的大小关系并说明理由;
(3)若点P在∠AOB的内部,上述结论还成立吗?写出此时的关系式.
分析 (1)根据轴对称的性质画出图形即可;
(2)连接OP1,根据轴对称的性质即可得出结论;
(3)根据(2)的证明过程可得出结论.
解答  解:(1)如图所示;
解:(1)如图所示;
(2)∠POP2=2∠AOB.
理由:∵点P关于直线OA的对称P1,点P1与P2关于直线OB的对称,
∴∠POD=∠DOP1,∠P2OE=∠P1OE,
∴∠POD+∠P2OE=∠DOP1+∠P1OE,即∠POP2=2∠AOB;
(3)点P在∠AOB的内部,结论∠POP2=2∠AOB还成立,
理由:如图1,
∵点P关于直线OA的对称P1,点P1与P2关于直线OB的对称,
∴∠POD=∠DOP1,∠P2OE=∠P1OE,
∴∠POP2=∠POE+∠P2OE
=∠P1OE+∠P2OE
=∠P1OD+∠POD+∠POE+∠POE
=2∠POD+2∠POE
=2∠AOB;
点评 本题考查的是作图-轴对称变换,熟知轴对称的性质是解答此题的关键.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
19.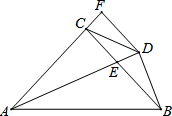 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:
①AE=2BD;②AB-AC=CE;③CE=2FC;
其中正确的结论有( )
 如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:
如图,在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于E,BD⊥AE于 D,DF⊥AC交AC的延长线于F,连接CD,给出三个结论:①AE=2BD;②AB-AC=CE;③CE=2FC;
其中正确的结论有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
14.下面各组线段中,能组成三角形的是( )
| A. | 5,2,3 | B. | 10,5,4 | C. | 4,8,4 | D. | 2,3,4 |
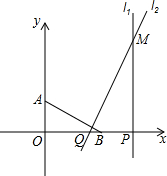 如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒
如图,点A(0,1)、B(2,0),点P从(4,0)出发,以每秒2个单位长度沿x轴向坐标原点O匀速运动,同时,点Q从点B出发,以每秒1个单位长度沿x轴向坐标原点O匀速运动,过点P作x轴的垂线l,过点Q作AB的垂线l2,它们的交点为M.设运动的时间为t(0<t<2)秒