题目内容
10.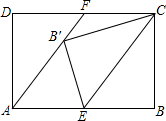 如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.
如图,已知矩形ABCD中,E是AB边的中点,连接CE,将△BCE沿直线CE折叠后,点B落在点B′处,连接AB′并延长交CD于点F.(1)求证:四边形AECF是平行四边形;
(2)若AB=6,BC=4,求tan∠CB′F的值.
分析 (1)认真审题,根据三角形的外角的性质,以及折叠的性质,可以证明∠FAE=∠CEB,进而证明AF∥EC,又AE∥FC,据此即可得证;
(2)由(1)知AF∥EC,所以∠CB′F=∠B′CE=∠BCE,进而得解.
解答 解:(1)∵四边形ABCD是矩形,
∴AE∥FC,
∵E是AB边的中点,
∴AE=BE,
∵△BCE沿直线CE折叠后,点B落在点B′处,
∴BE=B′E,
∴AE=B′E,
∵∠CEB=∠CEB′=$\frac{1}{2}∠BEB′$,
∴∠FAE=∠AB′E,
∴∠FAE=$\frac{1}{2}∠B′EB$,
∴∠FAE=∠CEB,
∴AF∥EC,
∴四边形AECF是平行四边形;
(2)∵AF∥EC,∠CB′F=∠B′CE,
∵△BCE沿直线CE折叠后,点B落在点B′处,
∴∠B′CE=∠BCE,
∴∠CB′F=∠B′CE=∠BCE,
∵四边形ABCD是矩形,
∴∠B=90°,
在Rt△EBC中,BE=$\frac{1}{2}AB$=3,BC=4,
∴tan∠BCE=$\frac{BE}{BC}$=$\frac{3}{4}$,
∴tan∠CB′F=$\frac{3}{4}$.
点评 本题主要考查了矩形的性质,平行四边形的判定,以及三角函数等知识点,解题的关键是把握住翻折变换前后角的大小不变,线段的大小不变,注意总结.

练习册系列答案
相关题目
20.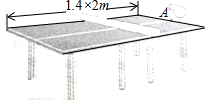 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
(1)当t为何值时,乒乓球达到最大高度?
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x-3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线恰好擦网扣杀到A,求a的值.
 某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:
某乒乓球馆使用发球机进行辅助训练,出球口在桌面中线端点A处的正上方,假设每次发出的乒乓球的运动路线固定不变,且落在中线上.在乒乓球运行时,设乒乓球与端点A的水平距离为x(米),与桌面的高度为y(米),运行时间为t(秒),经多次测试后,得到如下部分数据:| t(秒) | 0 | 0.16 | 0.2 | 0.4 | 0.6 | 0.64 | 0.8 | 6 |
| X(米) | 0 | 0.4 | 0.5 | 1 | 1.5 | 1.6 | 2 | … |
| y(米) | 0.25 | 0.378 | 0.4 | 0.45 | 0.4 | 0.378 | 0.25 | … |
(2)乒乓球落在桌面时,与端点A的水平距离是多少?
(3)乒乓球落在桌面上弹起后,y与x满足y=a(x-3)2+k.
①用含a的代数式表示k;
②球网高度为0.14米,球桌长(1.4×2)米.若球弹起后,恰好有唯一的击球点,可以将球沿直线恰好擦网扣杀到A,求a的值.
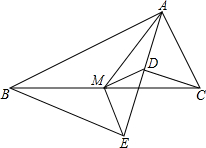 如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.
如图,Rt△ABC中,分别以AB、AC为斜边,向△ABC的内侧作等腰Rt△ABE、Rt△ACD,点M是BC的中点,连接MD、ME.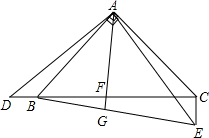 在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°.
在三角形ABC中,AB=AC,∠BAC=90°,∠DAE=90°. 如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).
如图,已知抛物线y=ax2+c与x轴交于点A、B,其中点A的坐标是(-1,0),与y轴交于点N(0,-1).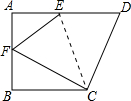 如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4.
如图,四边形ABCD中,AD∥BC,∠B=90°,将四边形ABCD沿CE折叠,使点D落在AB上的F点.若AB=BC=6,EF=5,∠FCD=90°,则AF长度为3或4. 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A按顺时针方向旋转60°到△ADE的位置,连接BD并延长交AE于F.