题目内容
2.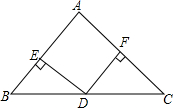 在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F
在△ABC中,AB=AC,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F(1)试判断四边形AFDE的形状并加以证明说明;
(2)只添加一个条件,使四边形EDFA是正方形,并说明理由.
分析 (1)四边形AFDE是以AD所在的直线为对称轴的四边形,只要证DE=DF,AE=AF即可;
(2)解决此题的关键是先假设四边形EDFA是正方形,根据其判定即可添加一个条件.
解答 (1)四边形AFDE是以AD所在的直线为对称轴的四边形;
证明:∵DE⊥AB,DF⊥AC,
∴∠DEB=∠DFC=90°.
∵AB=AC,
∴∠B=∠C.
又∵D是BC的中点,
∴DB=DC,
在△DEB和△DFC中,
$\left\{\begin{array}{l}{∠BED=∠CFD}\\{∠B=∠C}\\{DB=DC}\end{array}\right.$,
∴△DEB≌△DFC(AAS),
∴DE=DF,BE=CF,
∴AE=AF,
∴四边形AFDE是以AD所在的直线为对称轴的四边形.
(2)解:添加∠A=90°.
∵四边形AFDE是矩形,
又∵DE=DF,
∴四边形EDFA是正方形.
(方法很多,如∠B=45°或BC=$\sqrt{2}$AB或DE⊥DF或F为AC中点或DF∥AB等)
点评 此题考查了全等三角形的判定和正方形的判定,掌握正方形的判定方法与三角形全等的判定方法解决问题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
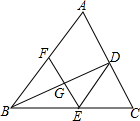 如图,BD是△ABC的平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.
如图,BD是△ABC的平分线,点E、F分别在BC、AB上,且DE∥AB,EF∥AC.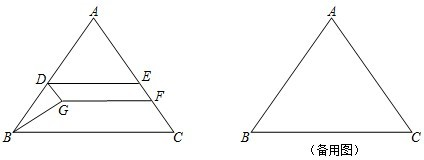
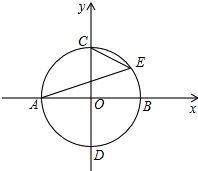 如图,在直角坐标系中,以坐标原点为圆心、半径为2的⊙O与x轴交于A,B两点,与y轴交于C,D两点.E为⊙O上在第一象限的某一点,直线BF交⊙O于点F,且∠ABF=∠AEC,则直线BF对应的函数表达式为y=-x+2,y=x-2..
如图,在直角坐标系中,以坐标原点为圆心、半径为2的⊙O与x轴交于A,B两点,与y轴交于C,D两点.E为⊙O上在第一象限的某一点,直线BF交⊙O于点F,且∠ABF=∠AEC,则直线BF对应的函数表达式为y=-x+2,y=x-2..