题目内容
9．
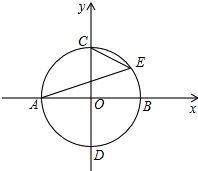如图，在直角坐标系中，以坐标原点为圆心、半径为2的⊙O与x轴交于A，B两点，与y轴交于C，D两点．E为⊙O上在第一象限的某一点，直线BF交⊙O于点F，且∠ABF=∠AEC，则直线BF对应的函数表达式为y=-x+2，y=x-2．．
分析 由题意可知，∠AEC=$\frac{1}{2}$∠AOC=45°；当∠ABF=∠AEC=45°时，只有点F与点C或D重合，根据待定系数法可求出直线BF对应的函数表达式．
解答 
解：根据圆周角定理得，∠AEC=$\frac{1}{2}$∠AOC=45°，
∵∠ABF=∠AEC=45°，
∴点F与点C或D重合；
当点F与点C重合时，设直线BF解析式y=kx+b，
则$\left\{\begin{array}{l}{b=2}\\{2k+b=0}\end{array}\right.$，
解得$\left\{\begin{array}{l}{k=-1}\\{b=2}\end{array}\right.$，
∴直线BF的解析式为y=-x+2，
当点F与点D重合时，同理可得y=x-2．
故答案为：y=-x+2，y=x-2．
点评 本题考查了圆周角定理的运用及待定系数法求解析式的方法．注意点F的位置，分类讨论．
练习册系列答案
相关题目
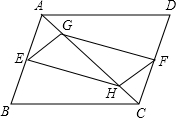如图，四边形ABCD为平行四边形，BE=DF，AG=CH．求证：四边形EHFG为平行四边形．
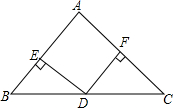在△ABC中，AB=AC，D是BC的中点，DE⊥AB，DF⊥AC，垂足分别是E，F
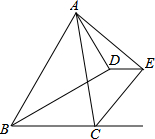在△ABC中，BD平分∠ABC，CE平分∠ACB的外角，AD⊥BD，AE⊥CE，若DE=$\frac{3}{2}$，AE=$\frac{7}{2}$，∠ABC=60°，则AB=5．
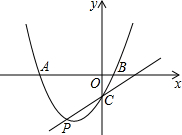如图，抛物线$y=\frac{1}{2}{x^2}+mx+n$交x轴于A、B两点，交y轴于点C，点P是它的顶点，点A的横坐标是-3，点B的横坐标是1．