题目内容
1. 如图,已知正方形ABCD中,点E是边BC上一点(不与B,C重合),连接AE,AC,将△AEC沿直线AE翻折,点C的对应点为点F,连接FE并延长FE交边CD于点G,若DG=3CG,则$\frac{CE}{BE}$=6.
如图,已知正方形ABCD中,点E是边BC上一点(不与B,C重合),连接AE,AC,将△AEC沿直线AE翻折,点C的对应点为点F,连接FE并延长FE交边CD于点G,若DG=3CG,则$\frac{CE}{BE}$=6.
分析 先过A作AH⊥FG于H,连接AG,构造全等三角形,再根据直角三角形,利用勾股定理列方程求解,即可得到BE,CE的长,进而得到$\frac{CE}{BE}$的值.
解答 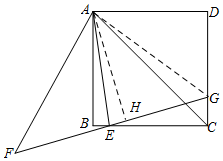 解:如图所示,过A作AH⊥FG于H,连接AG,则∠B=∠AHE=90°,
解:如图所示,过A作AH⊥FG于H,连接AG,则∠B=∠AHE=90°,
由折叠可得,∠AEF=∠AEC,而∠BEF=∠HEC,
∴∠AEB=∠AEH,
在△ABE和△AHE中,
$\left\{\begin{array}{l}{∠B=∠AHE}\\{∠AEB=∠AEH}\\{AE=AE}\end{array}\right.$,
∴△ABE≌△AHE(AAS),
∴BE=HE,AB=AH=AD,
在Rt△ADG和Rt△AHG中,
$\left\{\begin{array}{l}{AD=AH}\\{AG=AG}\end{array}\right.$,
∴Rt△ADG≌Rt△AHG(HL),
∴DG=HG,
设BC=CD=4,BE=HE=x,则CE=4-x,DG=HG=3,CG=1,
∵Rt△CEG中,CG2+CE2=EG2,
∴12+(4-x)2=(x+3)2,
解得x=$\frac{4}{7}$,
∴BE=$\frac{4}{7}$,CE=4-$\frac{4}{7}$=$\frac{24}{7}$,
∴$\frac{CE}{BE}$=6.
故答案为:6.
点评 本题主要考查了折叠问题,全等三角形的判定与性质以及勾股定理的综合应用,解决问题的关键是作辅助线,构造全等三角形,依据全等三角形对应边相等以及勾股定理列方程求解.

练习册系列答案
相关题目
16.某市政府将对江边一处废弃荒地进行绿化,要求栽植甲、乙两种不同的树苗共6000棵,且甲种树苗不得多于乙种树苗,某承包商以26万元的报价中标承包了这项工程.根据调查及相关资料表明:移栽一棵树苗的平均费用为8元,甲、乙两种树苗的购买价如表:
设购买甲种树苗x棵,承包商获得的利润为y元.请解答下列问题:
(1)求y与x之间的函数关系式;
(2)若栽植这批树苗全部成活,承包商要获得不低于中标价16%的利润,应如何选购树苗?最大利润是多少?
| 品种 | 购买价(元/棵) |
| 甲 | 20 |
| 乙 | 32 |
(1)求y与x之间的函数关系式;
(2)若栽植这批树苗全部成活,承包商要获得不低于中标价16%的利润,应如何选购树苗?最大利润是多少?
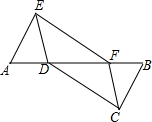 如图,四边形CDEF是平行四边形,点A、B在直线DF上,已知FB=AD,连接AE、BC.
如图,四边形CDEF是平行四边形,点A、B在直线DF上,已知FB=AD,连接AE、BC.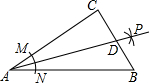 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交变BC于点D,若CD=4,AB=15,求△ABD的面积.
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交变BC于点D,若CD=4,AB=15,求△ABD的面积. 如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=BF,AF与DE相交于G.
如图,在正方形ABCD中,点E、F分别在AB、BC上,且AE=BF,AF与DE相交于G.