题目内容
9.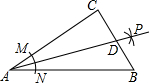 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交变BC于点D,若CD=4,AB=15,求△ABD的面积.
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC、AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AP交变BC于点D,若CD=4,AB=15,求△ABD的面积.
分析 根据题意可知AP为∠CAB的平分线,由角平分线的性质得出CD=DH,再由三角形的面积公式可得出结论.
解答  解:由题意可知AP为∠CAB的平分线,过点D作DH⊥AB于点H,
解:由题意可知AP为∠CAB的平分线,过点D作DH⊥AB于点H,
∵∠C=90°,CD=4,
∴CD=DH=4.
∵AB=15,
∴S△ABD=$\frac{1}{2}$AB•DH=$\frac{1}{2}$×15×4=30.
点评 本题考查的是作图-基本作图,熟知角平分线的作法是解答此题的关键.

练习册系列答案
相关题目
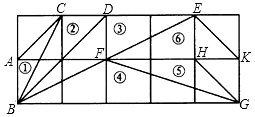 如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
如图,在正方形网格上有6个三角形:①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF. 如图,已知正方形ABCD中,点E是边BC上一点(不与B,C重合),连接AE,AC,将△AEC沿直线AE翻折,点C的对应点为点F,连接FE并延长FE交边CD于点G,若DG=3CG,则$\frac{CE}{BE}$=6.
如图,已知正方形ABCD中,点E是边BC上一点(不与B,C重合),连接AE,AC,将△AEC沿直线AE翻折,点C的对应点为点F,连接FE并延长FE交边CD于点G,若DG=3CG,则$\frac{CE}{BE}$=6.