题目内容
5．菱形具有、矩形却不具有的性质是（ ）| A． | 两组对边分别平行 | B． | 对角线互相平分 | ||
| C． | 对角线互相垂直 | D． | 对角线相等 |
分析 由菱形具有的性质是：两组对边分别平行，对角线互相平分，对角线互相垂直；矩形具有的性质是：两组对边分别平行，对角线互相平分，对角线相等；即可求得答案．
解答 解：∵菱形具有的性质是：两组对边分别平行，对角线互相平分，对角线互相垂直；矩形具有的性质是：两组对边分别平行，对角线互相平分，对角线相等；
∴菱形具有、矩形却不具有的性质是：对角线互相垂直．
故选C．
点评 此题考查了菱形的性质以及矩形的性质．注意熟记定理是解此题的关键．
练习册系列答案
心算口算巧算一课一练系列答案
相关题目
15．若y轴上的点A到x轴的距离为3，则点A的坐标为（ ）
| A． | （3，0） | B． | （3，0）或（-3，0） | C． | （0，3） | D． | （0，3）或（0，-3） |
13．-2的相反数是（ ）
| A． | -2 | B． | -$\frac{1}{2}$ | C． | 2 | D． | $\frac{1}{2}$ |
20．
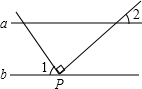如图，直线a∥b，直角三角板的直角顶点P在直线b上，若∠1=56°，则∠2为（ ）
如图，直线a∥b，直角三角板的直角顶点P在直线b上，若∠1=56°，则∠2为（ ）| A． | 24° | B． | 34° | C． | 44° | D． | 54° |
17．-$\frac{1}{2}$的绝对值是（ ）
| A． | 2 | B． | $\frac{1}{2}$ | C． | -2 | D． | -$\frac{1}{2}$ |