题目内容
10. 如图,小明想用镜子测量一棵古松树AB的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,第一次他把镜子放在点C处,人在点F处正好看到树尖A;第二次他把镜子放在点C′处,人在点F′处正好看到树尖A,已知小明眼睛距地面1.6m,量得CC′=7m,CF=2m,C′F′=3m,求这棵古松树AB的高.
如图,小明想用镜子测量一棵古松树AB的高,但因树旁有一条小河,不能测量镜子与树之间的距离,于是他两次利用镜子,第一次他把镜子放在点C处,人在点F处正好看到树尖A;第二次他把镜子放在点C′处,人在点F′处正好看到树尖A,已知小明眼睛距地面1.6m,量得CC′=7m,CF=2m,C′F′=3m,求这棵古松树AB的高.
分析 根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′,所以可得△BAC∽△FEC、△AC′B∽△E′C′F′,再根据相似三角形的性质解答.
解答 解:根据反射定律可以推出∠ACB=∠ECF,∠AC′B=∠E′C′F′,
∴△BAC∽△FEC、△AC′B∽△E′C′F′,
设AB=x,BC=y.
则$\left\{\begin{array}{l}{\frac{1.6}{x}=\frac{2}{y}}\\{\frac{1.6}{x}=\frac{3}{10+y}}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=16}\\{y=20}\end{array}\right.$.
答:这棵古松的高约为16米.
点评 本题考查相似三角形性质的应用,解题时关键是找出相似的三角形,然后根据对应边成比例列出方程,建立适当的数学模型来解决问题.

练习册系列答案
 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
 已知:如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC,求证:△ABD是等腰三角形.
已知:如图,△ABC中,AB=AC,∠BAC=120°,AD⊥AC,求证:△ABD是等腰三角形. 如图,AD是Rt△ABC斜边上的高,若AB=4cm,BC=10cm,求BD的长.
如图,AD是Rt△ABC斜边上的高,若AB=4cm,BC=10cm,求BD的长.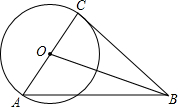 如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由.
如图,已知Rt△ABC中,∠C=90°,AC=12,tanA=$\frac{2}{3}$.以AC为直径作⊙O,又以点B为圆心,4为半径作⊙B,请判断⊙B与⊙O的位置关系,并说明理由. 如图,已知⊙A、⊙B和⊙C两两相切,已知AB=6cm,BC=5cm,AC=4cm,求这三个圆的半径.
如图,已知⊙A、⊙B和⊙C两两相切,已知AB=6cm,BC=5cm,AC=4cm,求这三个圆的半径.